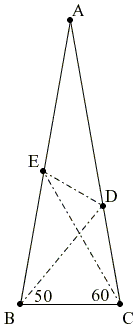
Let ABC be an isosceles triangle (AB = AC) with BAC = 20°. Point D is on side AC such that CBD = 50°. Point E is on side AB such that BCE = 60°. Find the measure of CED.

Solution

Copyright © 1996-2008 Alexander Bogomolny

The proof exploits the ideas used by Mariano Perez de la Cruz in solving a related problem.

Draw CF, F on AB, with BCF = 20°. Then ΔBFC is isosceles: BC = CF.

ΔBCD is also isosceles because

BDC = 180° - 80° - 50° = 50° = CBD

Hence, BC = CD and so CD = CF.

It follows that ΔCDF is isosceles with the apex DCF = 60°. Hence, ΔCDF is in fact equilateral.

Let CBD' = 60°, with D' on AC. P the intersection of BD' and CE. ΔCPB is equilateral and maps by a rotation around C onto ΔCDF. Therefore, if M is the intersection of DF and BP, CM is the bisector of ACB.

Now, consider a reflection in CM: D maps onto B, P onto F; let D' map on D'', D'' is on the extension of BC. Angle CFD'' (= CPD') = 120°, FCD'' = 20°. Thus CD''F = 40°. Angle FBD'' = 100° making BFD'' = 40° and Δ BFD'' isosceles: BF = BD''. Importantly, DP = DD'.

Since ΔAPD' is equilateral, the quadrilateral EPDD' is a kite, its diagonals are perpendicular. It follows that ED is the bisector of angles PED' and PDD'. In particular, PED = 30°.

In other words, CED = 30°.

Copyright © 1996-2008 Alexander Bogomolny