The 80-80-20 Triangle Problem, Solution #11

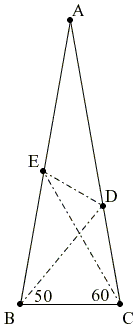
Let ABC be an isosceles triangle (AB = AC) with ∠BAC = 20°. Point D is on side AC such that ∠CBD = 50°. Point E is on side AB such that ∠BCE = 60°. Find the measure of ∠CED.

Solution

This solution is based on the trigonometric form of Ceva's theorem as suggested in [Prasolov, pp. 34-35].

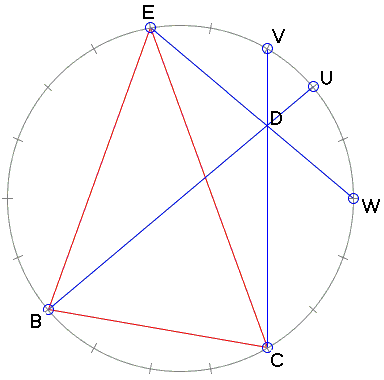
Imagine vertices of a regular 18-gon marked on its circumcircle. Several chords are drawn so that there is a triangle BCE, and chords BU, CV, EW that appear to meet in point D. Following [Prasolov], we are going to prove that they do.

By the trigonometric form of Ceva's theorem, the claim follows from the identity

sin(20°)·sin(50°)·sin(70°) = sin(30°)·sin(30°)·sin(80°),

which I am going to prove. There are a couple of useful trigonometric identities:

sinα sinβ = ½(cos(α - β) - cos(α + β)), and
sinα cosβ = ½(sin(α + β) - sin(α - β)), and

Both are simple consequences of the addition and subtraction formulas.

Since sin(30°)·sin(30°) = ½(1 - cos(60°)) = 1/4 and sin(20°)·sin(50°) = ½(cos(30°) - cos(70°)), the Ceva's identity reduces to

2 sin(70°)·(cos(30°) - cos(70°)) = sin(80°).

Let's keep applying the above formula again:

2 sin(70°)·(cos(30°) - cos(70°))	= sin(100°) + sin(40°) - sin(140°))
	= sin(80°) + sin(40°) - sin(40°))
	= sin(80°),

where a property of sine, viz., sin(180° - γ) = sin(γ), came in handy.

Now note that, if we continue BE and CV to their intersection at A, the latter diagram nicely overlays the diagram in the problem. This makes possible to read the value of ∠CED directly from the former: as an inscribed angle subtended by a 60° arc, ∠CED = 30°.

References

V. V. Prasolov, Essays On Numbers And Figures, AMS, 2000

The 80-80-20 Triangle Problem

41173624