Properties of the Harmonic Ratio

Points $C',$ $E,$ $C,$ $B$ lie on a line in this order. $D$ is a point not on the line. Then any two of the following conditions imply the third:

  1. The cross-ratio $(C'CEB)$ is harmonic: $(C'CEB)=-1.$

  2. $DE$ is angle bisector of $\angle C'DC.$

  3. $ED\perp BD.$

Proof $1,2\Rightarrow 3$:

From (1) it follows that (in terms of unsigned segments) $\displaystyle\frac{C'E}{CE}=\frac{C'B}{CB}.$ (2) implies that $\displaystyle\frac{C'E}{CE}=\frac{C'D}{CD}$ so that also $\displaystyle\frac{C'B}{CB}=\frac{C'D}{CD}.$ But this means that $DB$ is the external bisector of $\angle C'DC.$ Since the internal and external bisectors of an angle are perpendicular, $ED\perp BD.$

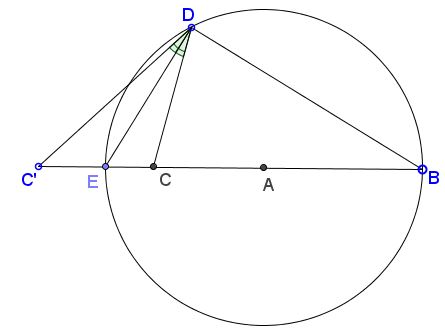
A View on the Circle of Apollonius - solution

Proof $1,3\Rightarrow 2$:

Since $\angle EDB$ is right, $EB$ is a diameter of circle $(EDB).$ From (1), and considering unsigned segments, $\displaystyle\frac{C'E}{CE}=\frac{C'B}{CB},$ implying that $EB$ is a diameter of the circle of Apollonius for the pair $C',C.$

For every point $P$ on the circle of Apollonius, $\displaystyle\frac{C'E}{CE}=\frac{C'P}{CP}=\frac{C'B}{CB}.$ In particular this is true for $D:$

$\displaystyle\frac{C'E}{CE}=\frac{C'D}{CD}=\frac{C'B}{CB},$

which exactly means that $DE$ is the internal, whereas $DB$ the external, angle bisectors of $\angle C'DC.$

Proof $2,3\Rightarrow 1$:

Since from (2) $DE$ is the angle bisector of $\angle C'DC,$ and from (3), $ED\perp BD,$ $BD$ is the external bisector of $\angle C'DC.$ Considering the sign segments, $\displaystyle\frac{C'E}{CE}=-\frac{C'B}{CB}$ such that $(C'CEB)=-1.$

Remark

The strange notations used above are supposed to remind of another property of the harmonic point pairs, viz.,

$(C'CEB)=-1$ iff the line $C'ECB$ passes through the center $A$ of a circle with diameter $EB$ and radius $R$ such that $C'$ and $C$ are inversive images of each other in $(A),$ meaning $C'A\cdot CA=R^2.$

Acknowledgment

This is Lemma 5 from an article Projective Geometry by Alexander Remorov, prepared for the IMO 2010 training camp. The solution is different from the one suggested there.

Cross-Ratio

  1. Cross - Ratio
  2. Ptolemy via Cross-Ratio
  3. Riemann Sphere and Möbius Transformation
  4. Complex Numbers and Geometry
  5. Projective Proof of Pascal's Theorem
  6. Butterfly Theorem
  7. Projective Proof of Maxwell's Theorem
  8. Chasles' Theorem, a Proof
  9. Harmonic ratio
  10. Properties of the Harmonic Ratio

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

72204383