A View on the Circle of Apollonius
What Might This Be About?
Problem
Given circle $(A)$ (centered at $A$ and its radius $R)$ and points $C,C'$ such that $CC'$ passes through $A.$ Let $E$ be the intersection of $CC'$ with $(A).$
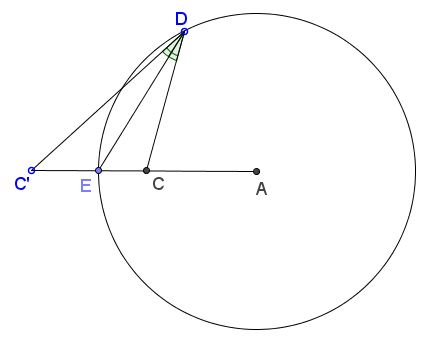
Then for any point $D$ on $(A)$ $\angle C'DE=\angle CDE$ if and only if $C$ and $C'$ are inverse images of each other in $(A):$ $AC\cdot AC'=R^2.$
Solution
Let $B$ be the second intersection of line $CC'$ with $(A),$ making $EB$ a diameter of $(A)$ and $\angle EDB$ right. Assuming $DE$ is the bisector of $\angle CDC',$ $DB$ is the exterior angle bisector at $D.$
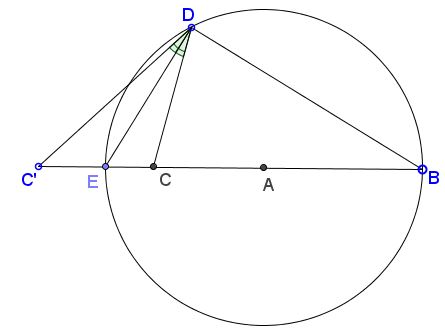
From the properties of angle bisectors, internal and external,
(1)
$\displaystyle \frac{C'E}{CE}=\frac{C'D}{CD}=\frac{C'B}{CB}.$
Assume (without loss of generality) that $C$ is inside the circle, $C'$ outside. Then
$C'E=AC'-R,\,CE=R-AC,\\C'B=AC'+R,\,CB=AC+R.$
So we can rewrite (1) as
$(AC'-R)(AC+R)=(R-AC)(AC'+R)$
which simplifies to $AC\cdot AC'=R^2.$
To prove the converse, the argument needs to be reversed.
Note that $(A)$ is the circle of Apollonius - the locus of point D, whose distances to the two given points $C$ and $C'$ are in a fixed ratio (here $CE/C'E$ has been fixed, since all three points have been given at the outset.) Thus the two given points ($C$ and $C')$ are the inversive images of each other in any circle of Apollonius defined by the third point ($E).$
In addition, observe that (1) implies $\displaystyle\frac{C'E}{CE}:\frac{C'B}{CB}=1$ which means that $B$ is the harmonic conjugate of $E$ with respect to the pair $C,C'.$ In other words, for the cross-ratio and signed segments $(CC'EB)=-1.$
Acknowledgment
The problem has been posted with solution by Dao Thanh Oai at the CutTheKnotMath facebook page.
The Circle of Apollonius
- Locus of Points in a Given Ratio to Two Points
- Line Not Through a Center of Similarity
- A View on the Circle of Apollonius
- Coaxal Circles Theorem
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73518527
