Ptolemy via Cross-Ratio

Mariano Perez de la Cruz
September 9, 2011

Recollect two well known properties of the cross-ratio.

1. Given four points on a plane if cross-ratio value (ABCD) = m, them the cross-ratio value, obtained by permutation the two interior points B and C, (ACBD) = 1 - m.
2. If complex numbers a, b, c, d represent points A, B, C and D, then the four points A, B, C, and D all belong to a same circle (or a straight line) iff the cross-ratio (abcd) is a real number.

For example, the cross-ratio (abcd) is the quotient of two single ratios (acd) = (a - c)/(b - c) and (bcd) = (a - d)/b - d). These single ratios are complex numbers L_a and L_b which may have different moduli, but always have same argument, provided the pairs of points {A, B} and {C, D} do not separate each other. Thus we see that

(acd) = (a - c)/(a - d) = (|a - c|/|a - d|) e^θ = L_a,
(bcd) = (b - c)/(b - d) = (|b - c|/|b - d|) e^θ = L_b.

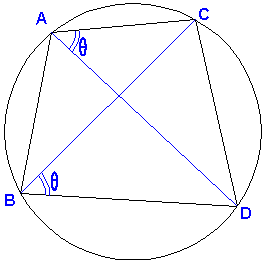
Indeed both arguments have the same value; we see the segment DC under the same angle θ either from A or B, as long as A, B, C and D are concyclic and A and B lay on the same side of segment CD. Therefore the quotient L_a/L_b of the two numbers L_a and L_b with the same arguments is real and equal to the ratio of their moduli, |La|/|Lb|. As a consequence, (ABCD) = (abcd), whenever points A, B, C, D are concyclic (or collinear) and the pairs {A, B} and {C, D} do not separate each other. In addition, in all eligible cases, (ABCD) = m > 0. It is convenient to order the points as in the above diagram.

The same procedure applies to the other cross-ratio (ACBD), and we see that also (ACBD) = (acbd). (So, too, (ACBD) = 1 - m > 0, implying in passing that 0 < m < 1.)

Ptolemy's theorem is just a direct consequence of the above and is equivalent to

(ABCD) + (ACBD) = 1.

Indeed, if we express the sides and the diagonals of the quadrilateral ABCD as the moduli of the related complex numbers: |a - c| = AC, |a - d| = AD, and so on, then (ABCD) + (ACBD) = 1 expands to

AC·BD / AD·BC + AB·CD / AD·BC = 1,

which is exactly Ptolemy's identity.

Ptolemy's Theorem

1. Ptolemy's Theorem
2. Sine, Cosine, and Ptolemy's Theorem
3. Useful Identities Among Complex Numbers
4. Ptolemy on Hinges
5. Thébault's Problem III
6. Van Schooten's and Pompeiu's Theorems
7. Ptolemy by Inversion
8. Brahmagupta-Mahavira Identities
9. Casey's Theorem
10. Three Points Casey's Theorem
11. Ptolemy via Cross-Ratio

|Contact| |Front page| |Contents| |Geometry| |Up| |Store|

Copyright © 1996-2012 Alexander Bogomolny