Importance of Having an Angle of 60 Degrees

Let $ABC$ be a triangle and $I$ its incenter. Assume $AB \lt AC$ and that $BI$ meets $AC$ in $E,$ while $CI$ meets $AB$ in $F.$

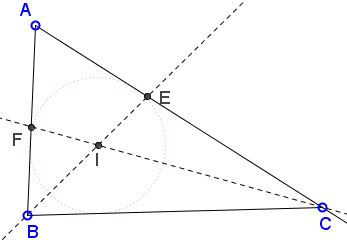
Importance of Having an Angle of 60 Degrees, problem

Then (we identify angles in triangle with vertices)

$\begin{cases} \text{If }A\lt\frac{\pi}{3}, & \text{then }EI\lt FI.\\ \text{If }A=\frac{\pi}{3}, & \text{then }EI=FI.\\ \text{If }A\gt\frac{\pi}{3}, & \text{then }EI\gt FI. \end{cases}$

Proof

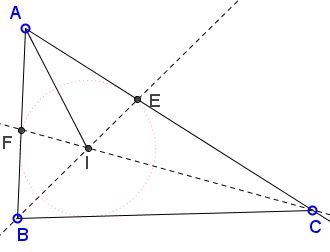
Importance of Having an Angle of 60 Degrees, solution

Since $AB\lt AC$ then $C\lt B$ and, since $A\lt \pi/3,$ then $B+C \gt B+C\gt\pi/3.$

On the other hand, $\displaystyle\angle AEI=C+\frac{B}{2}$ and $\displaystyle\angle AFI=B+\frac{C}{2},$ implying $\angle AEI+\angle AFI=\frac{3}{2}(B+C)\gt\pi.$ Obviously $\angle AEI\lt\angle AFI,$ so, by Leo Giugiuc's Trigonometric Lemma, $\sin\angle AEI\gt\sin\angle AFI.$

By the Law of Sines in triangles $AEI$ and $AFI,$

$EI\cdot\sin\angle AEI= AI\cdot\sin\angle\frac{A}{2}=FI\cdot\sin\angle AFI,$

and, since $\sin\angle AEI\gt\sin\angle AFI,$ $EI\lt FI.$

The other two cases are considered analogously. The second one is also dealt with on a separate page.

Acknowledgment

The statement above and its proof have been posted by Leo Giugiuc at the CutTheKnotMath facebook page. The lemma is a generalization of an earlier statement.

71537279