Construction of Thébault Circles
What Might This Be About?
Problem
Given $\Delta ABC$ and point $D$ on $BC.$
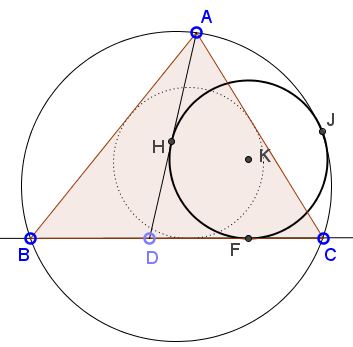
Construct a circle tangent to $AD,$ $CD,$ and the circumcircle of $\Delta ABC.$
Solution
Solution proceeds in several steps:
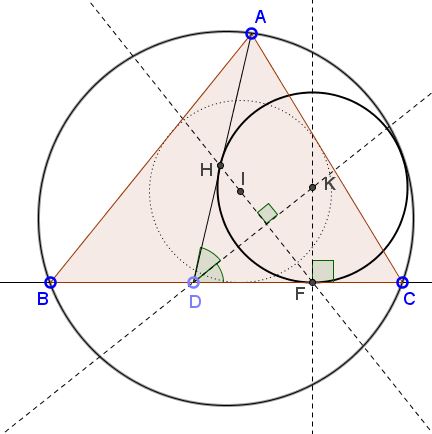
Find the incenter $I$ of $\Delta ABC.$
Drop a perpendicular from $I$ to the bisector of $\angle ADC.$ Mark its intersection with $BC$ - $F.$
- p>Erect a perpendicular to $BC$ at $F$. Mark $K$ - its intersection with the bisector of $\angle ADC.$
$K$ is the center of Thébault's circle.
For a proof, recollect Y. Sawayama's Lemma: If $F$ is the point of tangency of the Thébault circle $(K)$ and $BC$ then $IF$ passes through its point of tangency with $AD,$ say $H.$ But $FH$ is perpendicular to the bisector of $\angle ADC$ into which $(K)$ is inscribed.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73559644
