Circumcenter and Orthocenter Are Isogonal Conjugate
What is this about?
Problem
The bisector of angle at vertex $A$ of $\Delta ABC$ also bisects $\angle H_{a}AD,$ where $H_{a}$ is the foot of the altitude from $A,$ $AD$ is a diameter of the circumcircle $(ABC).$
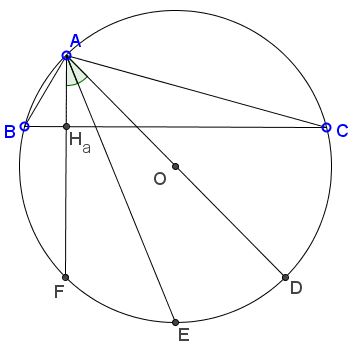
Proof
Let $F$ be the second intersection of the altitude $AH_{a}$ with $(ABC)$ and and $E$ the second intersection of the bisector. Let $M_a$ be the midpoint of $BC.$
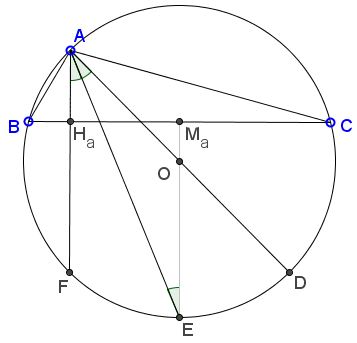
Then $O,$ $M_{a},$ $E$ are collinear. $\angle AEO=\angle EAO$ since $\Delta AEO$ is isosceles. Also, $\angle FAE=\angle AEO$ as alternate interior in parallel lines $AF$ and $EO.$ It follows that $\angle FAE=\angle EAO.$
Corollary
In any triangle the orthocenter and the circumcenter are isogonal conjugate of each other.
For a proof, one just needs to apply the definition and the above result to all three vertices of $\Delta ABC.$
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1966-2016 Alexander Bogomolny73564649
