Sidney Kung
Volume of a Hyperboloid of Two Sheets
A hyperboloid of two sheets is the surface obtained by revolving a hyperbola around its major axis. We are two find the volume as the result of revolving the portion \(AC\) of the hyperbola \(\displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) and the perpendicular \(CM\) around the \(y\)-axis.
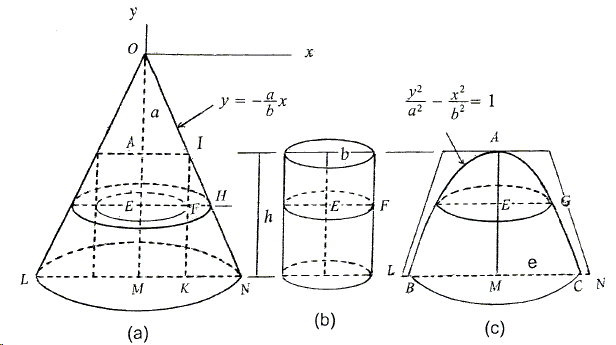
In part (a) of the diagram, \(OA=a\), \(OL\) and \(ON\) are asymptotes, \(AI=b\). Let \(IJ\perp LN\), and let a plane parallel to the base cut the solid, intersecting \(OM\), \(IJ\), \(ON\), and \(AC\) at \(E\), \(F\), \(H\), and \(G\), respectively. Let \(OY=y\) and \(EG=x\). Then, since \(\displaystyle\frac{b}{a}=\frac{EH}{y}\), or \(\displaystyle EH=\frac{b}{a}y\), \(\displaystyle x^2=\left(\frac{y^2}{a^2}-1\right)b^{2}=EH^{2}-AI^{2}\), or, \(EG^{2}=EH^{2}-EF^2\).
Hence, from (**), the volume of the hyperboloid (for the lower sheet) is the volume of the frustum of a cone minus the volume of the cylinder (parts (c) and (b) in the diagram above). Note that point \(C\) is on the hyperbola, \(OM=a+h\) so, \(\displaystyle (a+h)^{2}=\frac{a^2}{b^2}(b^{2}+e^{2})\), or \(\displaystyle h=\frac{a}{b}(\sqrt{b^{2}+e^{2}}-b)\). If \(h\) is very large, \(MN\) is close to \(e\). Thus, we get the volume
\(\displaystyle V_{HT}=\frac{1}{3}\pi h(b^{2}+be+e^{2})-\pi b^{2}h=\frac{\pi a}{3b}(e^{2}+be-2b)(\sqrt{b^{2}+e^{2}}-b).\)
![]()
- Cavalieri Principle
- A Generalized Cavalieri-Zu Principle
- Area, Sector Area, and Segment Area of an Ellipse
- Volume of a Sphere and Volume of an Ellipsoid
- Volume of an Elliptic Paraboloid
- Volume of a Hyperboloid of One Sheet
- Volume of a Hyperboloid of Two Sheet
- Volume of a Paraboloid of Revolution
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73580148
