Volume of a Sphere and Volume of an Ellipsoid

We give two ways to find the volume of a sphere. The first is to take a rectangular prism \(P\) of height equal to the radius \(R\) of a hemisphere \(S\).

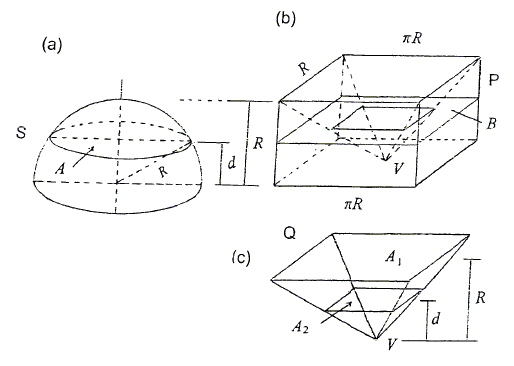
A 4-pyramid \(Q\) is inscribed into \(P\). A plane cuts the solids at a distance \(d\) from the base. Denote the cross-section areas of \(S\), \(P\), and \(Q\) by \(A\), \(A_1\), and \(A_2\), respectively. Since \(\frac{A_2}{A_1}=\frac{d^2}{R^{2}}\),

\(A=\pi (R^{2}-d^{2})=\pi R^{2}-\pi A_{2}R^{2}/A_{1}=A_{1}-A{2},\)

so, from (**), the volume of a sphere is

(4)

\(V_{S}=2\times (\pi R^{3}- \frac{\pi}{3}R^{2}R)=\frac{4}{3}\pi R^{3}.\)

The second way is to construct a wedge \(W\) whose dimensions are shown below

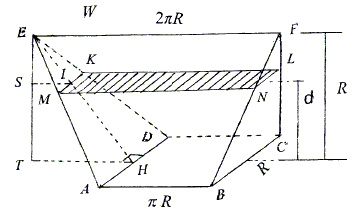
We find the cross-section area of \(W\) a distance \(d\) from the base as follows. Let \(ET\perp ABCD\) with foot \(T\), and let \(TH\perp AD\). Then we have

\(\displaystyle \frac{MK}{AD}=\frac{EI}{EH}=\frac{ES}{ET}=\frac{R-d}{R}\),

or \(MK=R-d\). It's easy to see that \(MN=\pi R +\pi d\). So, \((MK)(MN)=\pi (R^{2}-d^{2})=A\). We know that the volume of a wedge is given by the formula

(4')

\(\frac{1}{6}bh(2a+l).\)

where \(a\) and \(b\) are base lengths, \(l\) is the top edge length, \(h\) is the height of the wedge. Thus, by letting \(\pi R\), \(b=R\), \(l=2\pi R\), and \(h=R\) in (4') we obtain the volume of a sphere

\(V=2\times \left[\frac{1}{6}R\cdot R(2\pi R+2\pi R)\right]=\frac{4}{3}R^{3}.\)

To find the volume of an ellipsoid, we use a hemisphere instead of a cone [Needham] as a companion solid to a semi-ellipsoid.

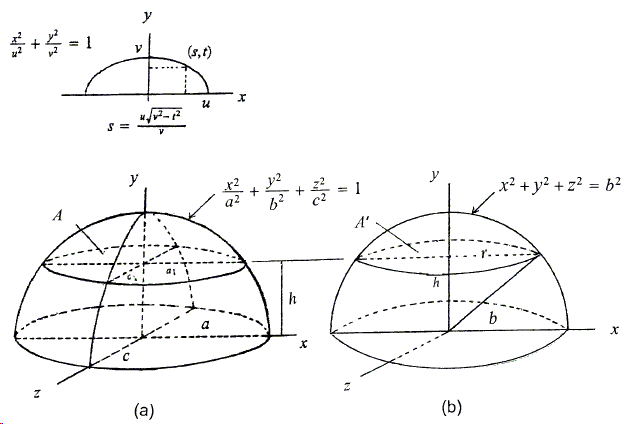
\(a_{1}\) and \(c_{1}\) are calculated based on the traces (semi-ellipses) on the \(by\)- and \(Hz\)-planes, respectively. \(a_{1}=\frac{a\sqrt{a^{2}-h^{2}}}{b}\) and \(c_{1}=\frac{ c\sqrt{b^{2}-h^{2}}}{b^{2}}\), \(A=\pi a_{1}c_{1}=\frac{\pi a}{b^{2}}(b^{2}-h^{2}) =\frac{a}{b^{2}}\pi r^{2}=\frac{a}{b^{2}}A'\). Hence, by (**), the volume of an ellipsoid is

(5)

\(\displaystyle 2\frac{ac}{b^{2}}(\frac{2}{3}\pi b^{3})=\frac{4}{3}\pi abc.\)

References

1. Joseph Needham, Science and Civilization of China, V.3, 1959, Caves Nooks, Taipei, 143.

• Cavalieri Principle
• A Generalized Cavalieri-Zu Principle
• Area, Sector Area, and Segment Area of an Ellipse
• Volume of a Sphere and Volume of an Ellipsoid
• Volume of an Elliptic Paraboloid
• Volume of a Hyperboloid of One Sheet
• Volume of a Hyperboloid of Two Sheet
• Volume of a Paraboloid of Revolution

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny