A Generalized Cavalieri-Zu Principle
Sidney Kung

Volume of an Elliptic Paraboloid

Consider an elliptic paraboloid as shown below, part (a):

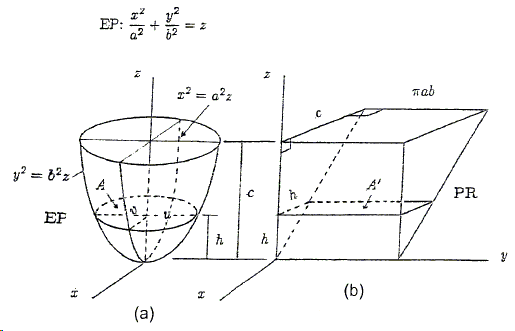
Volume of elliptic paraboloid by the Cavalier-Zu generalized principle

At \(z=h\) the cross-section is an ellipse whose semi-mnajor and semi-minor axes are, respectively, \(u\) and \(v\). Since \(u=b\sqrt{h}\), and \(v=a\sqrt{h}\), \(A=\pi abh\). We choose a triangular prism \(PR\) of height \(\pi ab\), and whose cross-section is an isosceles right triangle. At \(z=h\), \(A'=\pi abh=A\). Hence, from (**), the volume of \(EP\) is

\(\displaystyle V_{EP}=\frac{\pi abc^{2}}{2}\)

If the paraboloid is defined by a more dimesionally balanced equation like, say,

\(\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2}=\frac{z}{c}\)

then the volume of the paraboloid at height h will be given by

\(\displaystyle V_{EP}=\frac{\pi abh^{2}}{2c}\)

and, for \(h=c\),

\(\displaystyle V_{EP}=\frac{\pi abc}{2}.\)

71924430