A Generalized Cavalieri-Zu Principle
Sidney Kung

Volume of a Hyperboloid of One Sheet

A hyperboloid of one sheet is the surface obtained by revolving a hyperbola around its minor axis.

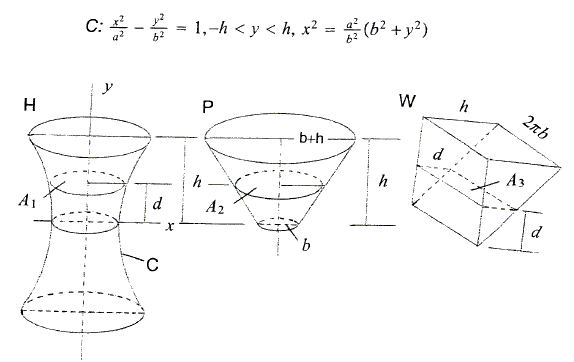
Volume of hyperboloid of one sheet by the Cavalier-Zu generalized principle

Denote the solid bounded by the surface and two planes \(y=\pm h\) by \(H\). At the level \(d\) above the \(x\)-axis, the cross-section of \(H\) is a circle of radius \(\displaystyle \frac{a}{b}\sqrt{b^{2}+d^{2}}\). So, \(\displaystyle A_{1}=\frac{\pi a^2}{b^2}(b^{2}+d^{2})\).

We place two solids \(P\) and \(W\) parallel to \(H\) on the \(x\)-axis. Their dimensions are chosen such that \(A_{2}=\pi (b+d)^{2}\) and \(A_{3}=2\pi bd\). Thus, \(\displaystyle A_{1}=\frac{\pi a^{2}}{b^2}[(b+d)^{2}-2bd]=\frac{a^2}{b^2}(A_{2}-A_{3})\). Hence, by (**), the volume of the hyperboloid \(H\) is \(\displaystyle 2\times\frac{a^2}{b^2}[\mbox{volume of}\space P-\mbox{volume of}\space W\space ]\), which is

\(\displaystyle V_{H}=\frac{2a^2}{b^2}\{\frac{\pi h}{3}[(b+h)^2+b(b+h)+b^{2}]-\pi h^{2}b\}=\frac{2\pi ha^2}{b^2}\left(b^{2}+\frac{h^2}{3}\right).\)

71534375