A Generalized Cavalieri-Zu Principle
Sidney Kung

Volume of a Paraboloid of Revolution

We are to find the volume of a solid generated by revolving the region bounded by the parabola \(y^{2}=2px\) \((p\gt 0)\) and \(x=c\) \((c\gt 0)\) about the \(x\)-axis. The cross-section of a vertical plane (cutting through point \((0,x_{1})\)) and the solid is a circle of radius \(\sqrt{2px_{1}}\) produced.

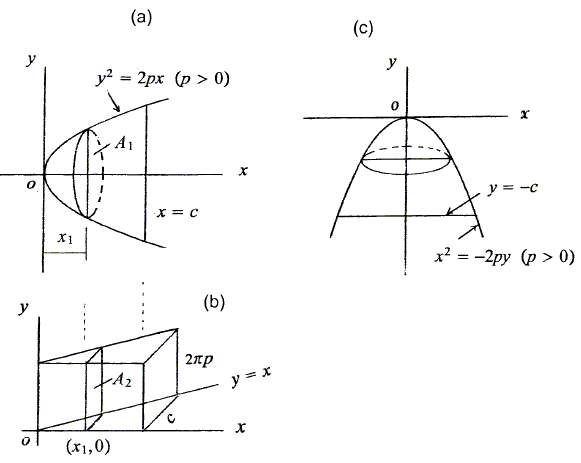
Volume of a Paraboloid of Revolution by the Cavalier-Zu generalized principle

Now if we construct a triangular rism of height \(2\pi p\), with base area bouned by \(y=x\), \(x=c\), and the \(x\)-axis, then the area of the cross-section at \(x=x_{1}\) is \(A_{2}=2\pi px_{1}\). Hence, by (**), the volume of the solid of revolution is \(\frac{1}{2}(c^{2}\cdot 2\pi p)=\pi pc^2\). Similarly, the Volume of a Paraboloid of Revolution by revolving a region bounded by the parabola \(x^{2}=-2py\) \((p\gt 0)\) and \(y=-c\) \((c\gt 0)\) about the \(y\)-axis is \(\pi pc^2\).

71560680