Two Triangles Inscribed in a Conic - with Solution

Hubert Shutrick

Here is a proof of the theorem that was suggested by Vladimir Nikolin.

Two triangles \(ABC\) and \(DEF\) intersect at points \(H = AB \cap FD\), \(I = FD \cap BC\), \(J = BC \cap DE\), \(K = DE \cap CA\), \(L = CA \cap EF,\) \(G = EF \cap AB\).

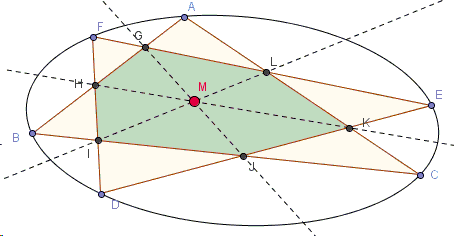
wo triangles inscribed in a conic

Prove that \(A\), \(B\), \(C\), \(D\), \(E\), \(F\) lie on a conic if and only if the lines \(HK\), \(IL\) and \(JG\) are concurrent.

The proof is based on the properties of involutions. If \(A,\) \(B,\) \(C,\) \(D,\) \(L,\) \(G\) are considered as fixed points, the pencil of conics through \(A,\) \(B,\) \(C,\) \(D\) intersects the line \(LG\) in pairs of points in involution. The theorem will be proved if it can be shown that this involution can be replicated using the intersections of the lines. The three degenerate conics in the pencil are the pairs of lines \((BC,\,AD)\), \((AB,\,CD)\) and \((BD,\,AC)\) and their intersections with \(LG\) give three pairs of the involution. It will then be sufficient to find a projectivity from the line \(LG\) to itself that agrees with these three pairs.

The usual way of defining a projectivity on the line would be to find a construction taking a point \(E\) on the line to its corresponding point \(F\). This doesn't seem to be easily done so we seek the relation between \(E\) and \(F\) that is given by the concurrency of the lines. For points \(E\) and \(F\) on \(LG\), let \(ED\) meet \(BC\) and \(CA\) at \(J\) and \(K\) respectively and let \(FD\) meet \(BC\) and \(AB\) at \(I\) and \(H\) respectively. The claim is that, if \(E\) and \(F\) are distinct and the lines \(HK,\, IL\) and \(JG\) are concurrent, then \(E\) and \(F\) are pairs of the involution.

(The applet below illustrates the proof. Points \(E\) and \(F\) are draggable.)

Proof

The applet allows the points \(E\) and \(F\) to be slid independently along the line \(GL\). It is instructive to move one of them keeping the other fixed to see how the other points and lines move. Slide them towards a pair that is given by one of the degenerate conics and observe what happens. For instance, if \(E\) is on \(AC\) and \(F\) is on \(BD\), then the lines \(HK\) and \(IL\) coincide so the concurrency occurs. Let \(F\) approach \(E\) and note that concurrency always occurs since \(FD = ED\). Note also that there seems to be just one other point \(F\) for concurrency for each \(E\). This suggests that, if we express \(GL\) in parametric form, the relation between the parameters for \(E\) and \(F\) should be quadratic in each.

Assuming homogeneous coordinates, let a point be represented by an ordered triple \(\textbf{u} =(x,y,z)\). The points \(E\) and \(F\) can be described in the parametric form \(\textbf{u} + s\textbf{v}\) and \(\textbf{u} + t\textbf{v}\) respectively. The points \(K\) and \(J\) will take the form \(\textbf{k} + s\textbf{k}'\) and \(\textbf{j} + s\textbf{j}'\) and the points \(H\) and \(I\) will take the form \(\textbf{h} + t\textbf{h}'\) and \(\textbf{i} + t\textbf{i}'\). Coefficients for the equations of lines can also be written as triples so the line \(GJ\) will depend only on \(s\) and be described by \(\textbf{p} + s\textbf{p}'\) forming a pencil of lines as \(s\) varies and similarly the line \(LI\) will be described by \(\textbf{q} + t\textbf{q}'\). Since the coefficients for the line \(HK\) are determinants of order \(2\) in the coordinates of the points, they will take the form \(\textbf{r} + s\textbf{r}' + t\textbf{r}'' + st\textbf{r}'''\). The condition that the lines are concurrent is then that the determinant that has these triples as rows is zero. It would be very complicated to calculate this determinant from the given fixed points but it will be a polynomial of the form \( a +bs +ct+dst+es^{2}t +fst^{2} +gs^{2}t^{2}\).

However, \(F=E\) satisfies the concurrency condition for all \(E\) and therefore \(a+(b+c)s+ds^{2}+(e+f)s^{3}+gs^{4}\) is zero for all values of \(s\) implying that \(a=0,\) \(c=-b,\) \(d=0,\) \(f=-e,\) \(g=0\).

The condition becomes \(b(s-t)+est(s-t)=0\) so \(t=b/es\), an involution.

(Another solution is available that makes repeated use of the trigonomeric form of Ceva's theorem.)

Pascal and Brianchon Theorems

71535979