Two Triangles Inscribed in a Conic
The following observation has been made by Vladimir Nikolin from Serbia
Let \(ABC\) and \(DEF\) be two triangle inscribed in the same conic. Their sides intersect in six points \(G, H, I, J, K, L\) as in the diagram.
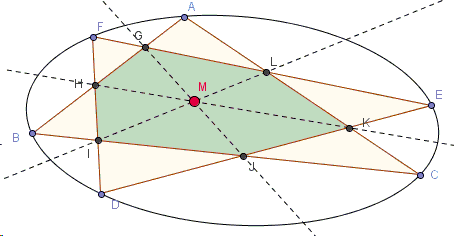
Prove that the lines \(GJ\), \(HK\), and \(IL\) are concurrent.
The applet below serves a dynamic illustration. (The five points that define the ellipse can be displayed and then dragged by checking the "Show 5 pins" box. In case not all intersections of the sides of the triangles are clearly identified, check the box "Show lines".)
Proof
Let \(ABC\) and \(DEF\) be two triangle inscribed in the same conic. Their sides intersect in six points \(G, H, I, J, K, L\) as in the diagram.

Prove that the lines \(GJ\), \(HK\), and \(IL\) are concurrent.
The three lines in question are Pascal's lines of three hexagons obtained from \(ABCDEF\) by permutation of indices.
Indeed, \(H=AB\cap EF\) while \(K=AC\cap DE\) such that \(HK\) is the Pascal line of the hexagon \(ABEDFC\). (The intersection of \(AD\) and \(BE\) would be the third point on that line. But we do not need it here.)
Lines \(AC\) and \(DF\) intersect in \(L\), while \(BC\) and \(DF\) intersect in \(I\), making \(IL\) the Pascal line of hexagon \(ACBEFD\).
Finally, \(G=AB\cap EF\) and \(J=BC\cap DE\), meaning that \(GJ\) is the Pascal line of hexagon \(ABCFED\).
However, the proposition does not seem to fall under either Steiner's or Kirkman's theorems covering concurrence of triples of Pascal Lines of an inscribed hexagon \(AFBDCE\). For now it's a mystery that might have excited Pascal himself.
Pascal and Brianchon Theorems
- Pascal's Theorem
- Pascal in Ellipse
- Pascal's Theorem, Homogeneous Coordinates
- Projective Proof of Pascal's Theorem
- Pascal Lines: Steiner and Kirkman Theorems
- Brianchon's theorem
- Brianchon in Ellipse
- The Mirror Property of Altitudes via Pascal's Hexagram
- Pappus' Theorem
- Pencils of Cubics
- Three Tangents, Three Chords in Ellipse
- MacLaurin's Construction of Conics
- Pascal in a Cyclic Quadrilateral
- Parallel Chords
- Parallel Chords in Ellipse
- Construction of Conics from Pascal's Theorem
- Pascal: Necessary and Sufficient
- Diameters and Chords
- Chasing Angles in Pascal's Hexagon
- Two Triangles Inscribed in a Conic
- Two Triangles Inscribed in a Conic - with Solution
- Two Pascals Merge into One
- Surprise: Right Angle in Circle
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73609268
