A Game of Candy Squares
This two-player game starts with two heaps of candy squares. To make a move, a player gobbles one heap and divides the other one into two. The players take turns; the one who can't move, i.e., divide a heap, loses the game. Is there a strategy to win the game?
In the applet below, the game is played against the computer. To divide a heap just click somewhere between two squares. The other heap will automatically disappear. If you wish the computer to make the first move press the "You start" button.
| What if applet does not run? |
|Activities| |Contact| |Front page| |Contents| |Games|
Copyright © 1996-2018 Alexander Bogomolny
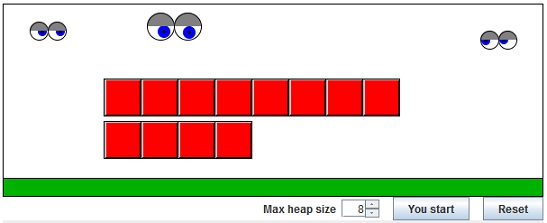
An easily overlooked but crucial fact is that one of the two present heaps disappears on a move and thus has no bearings on the game, except, of course, that up front one may not know which one of the two heaps is less important than the other.
We are going to prove that the player who faces a situation in which at least one of the heaps has an even number of squares has a winning strategy.
For convenience, let's call the configuration of two heaps of which at least one has an even number of squares P-position. Let's call all others N-position. And let's denote positions by the lengths of their heaps, i.e., by a pair of integers
Statement
Every move in an N-position - different from the final (1, 1) - leaves a P-position. In any P-position, there is a move that leaves an N-position.
Proof
Assume both n and m are odd, i.e., (n, m) is an N-position. If both n and m are greater than 1, there is a choice to make. Otherwise, the player will split the larger heap and consume 1 square. Any split of a heap with an odd number of squares leaves one even heap, i.e., a P-position.
Assume n is even, so that (n, m) is a P-position. It is always possible to split n into the sum of two odd numbers and consume the m-heap. The position left is an N-position.
References
- A Decade of the Berkeley Mathematical Circle, The American Experience, Volume I, Z. Stankova, Tom Rike (eds), AMS/MSRI, 2008, p. 159
|Activities| |Contact| |Front page| |Contents| |Games|
Copyright © 1996-2018 Alexander Bogomolny73580823
