Dawson's Chess
Dawson's Chess was invented in 1930s and is played with one or more heaps of items. The nature of the items is not important, but as in the game of Kayles they are referred to as Skittles. In the applet below, they are positioned on a circle, with the number of positions shown in the upper right portion of the applet. This may be specified by clicking a little off the vertical axis of the number. (Clicks to the left of the axis decrease the number, to the right increase it.)
To remove a skittle just click on it. However, the rules devised by T. R. Dawson stipulate that, the immediate neighbors - if any - of a skittle that was clicked on are also removed. So that, depending on the configuration, a player may remove 1, 2, or 3 skittles.
| What if applet does not run? |
|Activities| |Contact| |Front page| |Contents| |Games|
Copyright © 1996-2018 Alexander BogomolnyDawson's Chess
Dawson's chess can be played (and this explains the chess part in the name) on a 3×n chess-like board with two rows (White and Black) of pawns. Like in chess, pawns move forward vertically and capture diagonally. Capturing is obligatory.
Here is a starting position on a 3×9 board.

|
After White moves the e-pawn (followed by the reciprocal captures from d and f) and Black moves the a-pawn (followed by the reciprocal captures from b) the position changes to
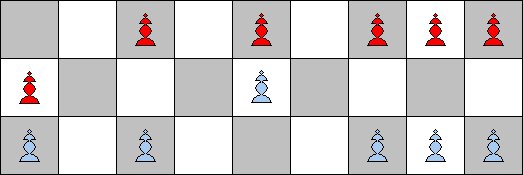
|
In the applet, this game is equivalent to starting with 9 (not connected) skittles and hitting the skittles number 5 and 1, which leaves a lone skittle in the position 3 and three adjacent skittles in positions 7, 8, and 9.
The game ends when no skittles are left over. The Grundy number for an empty board is 0. For a single skittle it is 1. For other sizes, the Grundy numbers are found via the Mex rule. Here is a partial table:
| 0-9 | 0 1 1 2 0 3 1 1 0 3 | |
|---|---|---|
| 10-19 | 3 2 2 4 0 5 2 2 3 3 | |
| 20-29 | 0 1 1 3 0 2 1 1 0 4 | |
| 30-39 | 5 2 7 4 0 1 1 2 0 3 | |
| 40-49 | 1 1 0 3 3 2 2 4 4 5 | |
| 50-59 | 5 2 3 3 0 1 1 3 0 2 | |
| 60-69 | 1 1 0 4 5 3 7 4 8 1 | |
| 70-79 | 1 2 0 3 1 1 0 3 3 2 | |
| 80-89 | 2 4 4 5 5 9 3 3 0 1 | |
| 90-99 | 1 3 0 2 1 1 0 4 5 3 | |
As usual, the P-positions are those whose Grundy number is 0. You are bound to win the game if, on every move, you leave a P-Position.
References
- E. R. Berlekamp, J. H. Conway, R. K. Guy, Winning Ways for Your Mathematical Plays, Volume 1, A K Peters, 2001
- R. Guy, fair game, Comap's Explorations in Mathematics, 1989
|Activities| |Contact| |Front page| |Contents| |Games|
Copyright © 1996-2018 Alexander Bogomolny73591114
