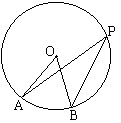
This is a well known fact that an angle inscribed into a circle measures half the central angle subtending the same arc: AOB = 2·APB. This is Proposition III.20 from Euclid's Elements which we already used in several places: Sine, Cosine, and Ptolemy's Theorem, Longest segment, Ptolemy's Theorem, Generalization of Napoleon's Theorem. (A proof and a dynamic illustration are avaiable elsewhere.)

Proposition III.21 gives us an inevitable conclusion that all inscribed angles in the same circle subtending the same arc are equal. Thus, APB = AQB.

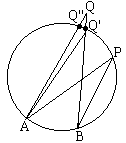
Turning the proposition around, is it true that if APB = AQB, then there exists a circle that passes through all four points A, B, P, and Q? Yes, it is. To see this, inscribe APB into a circle. A priori point Q then may lie either inside or outside this circle or on its circumference. But the former two cases are impossible. There are several possible configurations with Q outside the circle. I'll consider only the one depicted in the diagram (and skip the case when Q is inside the circle.) By Proposition I.16, AQ'B > AQB. (Proposition I.16 states that the exterior angle of a triangle is greater than either of the interior and opposite angles. This applies to AQQ' and its exterior angle AQ'B.) But, as we already know, AQ'B = APB. Which is a contradiction. Therefore, the point Q lies on the circle through A, B, and P.

(Restricting the question a little bit, is it true that, in a triangle ABC, the points B, C, H_b, and H_c lie on the same circle?)

This conversion of Proposition III.21 admits a reformulation: the locus of all points P such that APB is equal to a given angle consists of two circular arcs symmetric with respect to the segment AB. The two arcs merge into a circle when the angles at hand are right.

When the angles APB are right, the triangles APB are right and AB serves as the common hypotenuse of the triangles and as a diameter of the circle. In other words, the locus of the third vertices P of right triangles APB with a fixed hypotenuse AB is a circle with diameter AB.

Let's change our view point once more. Consider the family of straight lines passing through point A. (Such a family is known as a pencil of lines.) For each line in the pencil, consider the foot of the perpendicular from point B on to the line. What is the locus of the foot of the perpendicular from B onto lines from a given pencil through A? Why, the circle, of course. (This is known as Thales' Theorem: an angle inscribed in a semicircle is right, and vice versa.) The formulation is different but the result is the same.

One way to visualize a pencil of lines is to think of a single line that rotates around a fixed center. As the line rotates around point A, we mark the foot of the perpendiculars dropped onto the line from point A. We know that the locus of the marked points is a circle. Note now that we may also consider the perpendicular as a whole. As the line rotates around A, the perpendicular onto the line from B rotates around B. What can be said about these two motions?

Recollect our starting point, the equality APB = AQB. In the configuration of 4 points A, B, P, and Q, this is not the only pair of inscribed angles whose equality is implied by Proposition III.21. Look at the illustration. The two angles QAP and QBP also subtend the same arc and, therefore, are equal, QAP = QBP.

We get the following interpretation. Let a line through a point A rotate around A with a constant angular speed. Let another line rotate around another point B with the same angular speed. Then, at any point in time, the angle formed by the two rotating lines remains the same. Indeed, fix a time interval. During this interval let the first line move from the position AP to the new position AQ. The second line changes from BP to BQ. Since angular velocities of the two lines are equal, QAP = QBP. As we know, this means that the 4 points P, Q, A, and B lie on the same circle. Fixing A, B, and P, and letting Q change we observe that the point of intersection of two lines rotating with equal angular velocities describes a circle. (A dynamic illustration is available elsewhere.)

We can use the above diagram to make an observation concerning cyclic quadrilaterals: in a convex quadrilateral ABPQ the opposite sides add up to 180^o. In a self-intersecting quadrilateral APBQ, the opposite angles are equal.