A Property of Thébault Circles
What Might This Be About?
Problem
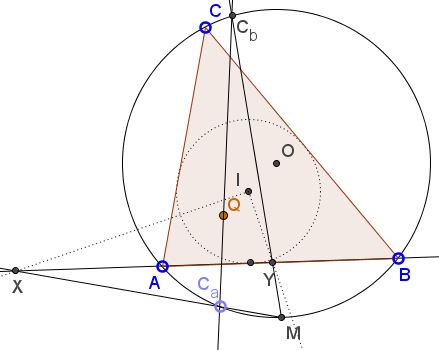
Given $\Delta ABC$ and point $D$ on $AB.$ Construct two Thébault circles $(K_{A})$ and $(K_{B})$ and their points of tangency with the circumcircle, $C_A$ and $C_B.$
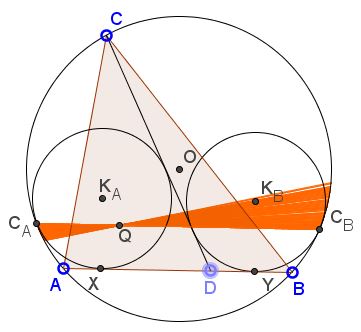
When $D$ changes line $C_AC_B$ passes through a fixed point. This fixed point the external center of similitude of the incircle $(I)$ and the circumcircle $(O).$ This is point $X_{56}$ in C. Kimberling's Encyclopedia of Triangle Centers.
Solution 1
Label $(K_A),$ $(K_B)$ the Thébault circles of the cevian $CD.$ $(K_A)$ touches $AB$ at $X$ and the circumcircle $(O)$ at $C_A$ while $(K_B)$ touches $AB$ at $Y$ and the circumcircle at $C_B.$ Circles $(O)$ and $(K_B)$ are homothetic at $C_B.$ This homothety maps $Y$ onto point $M$ on $(O)$ and the line $AB$ tangent to $(K_B)$ at $Y$ to the line tangent to $(O)$ at $M$ and thus parallel to $AB.$ Since the point of tangency of a line tangent to a circle and parallel to a chord divides the arc subtended by the chord in half, it follows that $M$ is the midpoint of the arc $AB.$ Note that $C_B,$ $K_B,$ and $O$ are collinear.
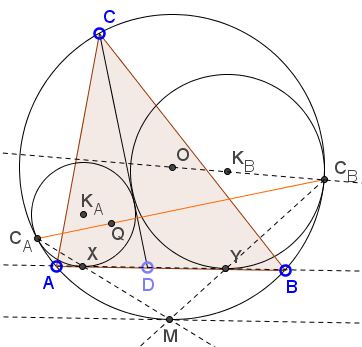
Similarly, $C_AX$ passes through $M$ and this is where the two lines $C_AX$ and $C_BY$ meet. Note that $C_A,$ $K_A,$ and $O$ are collinear.
By Sawayama's lemma, for the incenter $I$ of $\triangle ABC$ we have $IX \perp IY.$
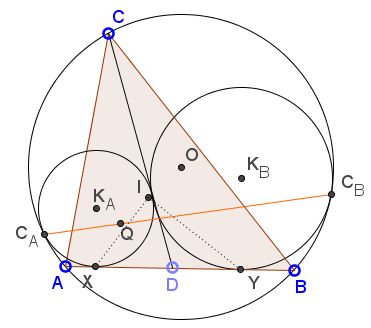
The function defined on the pencil of lines through $I$ that maps pairs of orthogonal lines onto each other is an involution. So lines $IX,$ $IY$ are in involution. This also defines an involution on line $AB$ that maps $X$ into $Y$ (and vice versa), and an involution on the pencil through $M$ that maps $MX$ onto $MY,$ i.e., $MC_A$ onto $MC_B.$ The latter defines an involutive homography on points of $(O),$ with $C_A$ and $C_B$ being mapped onto each other. All lines $C_AC_B$ pass through the fixed pole of the homography, say, $P.$
There is an additional homothety, viz., that which maps $(I)$ onto $(O).$ Denote its center $Q.$ If $F$ is the point of tangency of $(I)$ with $AB$ then this homothety takes $F$ to $M,$ such that $Q,$ $F,$ $M$ are collinear. In other words, $Q$ is the intersection of $IO$ and $FM.$ It now suffices to show that $P=Q.$
To this end consider the case where, say, $C_A$ lies on $IO.$
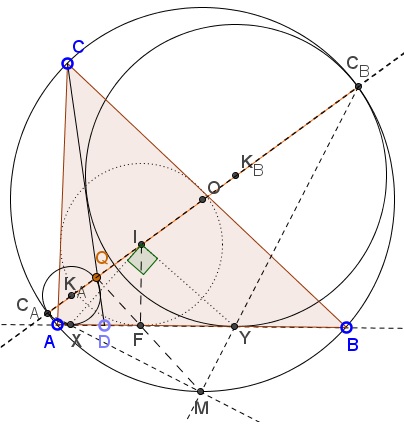
This implies that points $C_A,$ $I,$ $K_A,$ $O$ (and $Q!$) are collinear. By Th&eacte;bault's theorem, $K_A,$ $I,$ and $K_B$ are always collinear. Thus it follows that in case where $C_A$ lies on $IO,$ so does $K_B$ and, therefore $C_B.$ We conclude that, in this case, $Q$ lies on $C_AC_B$ and, $P$ lies on $IO.$ But $P$ is independent of $D$ which tells us plainly that $P\in IO.$
The proof would be finished if also $P\in FM,$ or $Q\in C_AC_B$ for some other position of $D,$ i.e., $C_A$ and $C_B.$ Such poistion indeed exists, but to observe it we need to extend the involution $C_A\leftrightarrow C_B$ to allow those points on the other side of $AB.$ We proceed to construct such an extension:
Start with $C_A\in (O).$ Let $X=C_AM\cap AB.$ Define $Y\in AB$ such that $IX\perp IY.$ Set $C_B=MY\cap (O).$ As we just saw, properties of Thébault's circles and Sawayama's lemma insure that this construction complies with the one above.
But, having the extension, we may let $C_A$ to coincide with $M.$ As, $C_A$ approaches $M,$ $X$ moves to infinity, eventually making $IX$ parallel to $AB,$ and implying that $Y=F,$ the point of tangency of $(I)$ and $AB.$ But then $C_B=FM\cap (O),$ so that $C_AC_B$ passes through $Q$ (and also, as always, $P.)$ We conclude that $P=Q,$ as expected.
Solution 2
Introduce
$S$ - intersection of $K_{A}K_{B}$ and $AB$
$I$ - incenter of triangle $ABC$
$O$ - circumcenter of triangle $ABC$
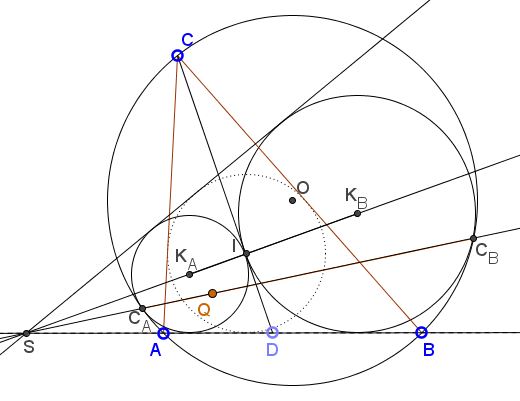
By Thebault theorem,we deduce that $K_{A},$ $I,$ $K_{B}$ are collinear, so the external center of similitude of $(I)$ and $(K_{A})$ and the external center of similitude of $(K_{A})$ and $(K_{B})$ coincide with each other. Because $C_{A}$ is the external center of similitude of $(K_{A})$ and $(O),$ $S$ is the external center of similitude of $(I)$ and $(K_{A}).$ By Monge's theorem (consider $(I),$ $(O)$ and $(K_{A})),$ we deduce that $SC_{A}$ pass through the external center of similitude of $(I)$ and $(O),$ namely $X(56).$ By same reason we can deduce that $S,$ $C_{B},$ $X(56)$ are collinear, so $C_{A}C_{B}$ pass through $X(56),$ which is a fixed point:P $Q=X(56).$
Acknowledgment
The problem has been posted by Dao Thanh Oai (Vietnam) at the CutTheKnotMath facebook page and GeoGebra tube. The solution is due to Hubert Shutrick. A more formal, but the one which is beyond my uderstanding, could be found at the artofproblemsolving site. The second solution is due to Telv Cohl.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny71550626
