$\pi$ in Pascal's Triangle via Triangular Numbers

An unusual series that produces $\pi$ was discovered by Jonas Castillo Toloza in 2007; the series consists of the reciprocals of the triangular numbers and, as such, could be detected in Pascal's triangle:

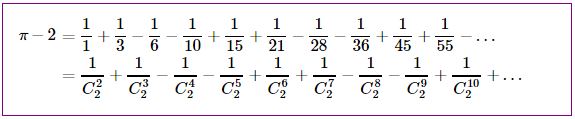
$\begin{align}\displaystyle \pi-2&=\frac{1}{1}+\frac{1}{3}-\frac{1}{6}-\frac{1}{10}+\frac{1}{15}+\frac{1}{21}-\frac{1}{28}-\frac{1}{36}+\frac{1}{45}+\frac{1}{55}-\ldots\\ &=\frac{1}{C^{2}_{2}}+\frac{1}{C^{3}_{2}}-\frac{1}{C^{4}_{2}}-\frac{1}{C^{5}_{2}}+\frac{1}{C^{6}_{2}}+\frac{1}{C^{7}_{2}}-\frac{1}{C^{8}_{2}}-\frac{1}{C^{9}_{2}}+\frac{1}{C^{10}_{2}}+\ldots \end{align} $

Below, I give it two proofs: a short one that reduces it to Nilakantha's series, and another, due to Jonas Castillo Toloza, that thus gives an independent derivation of the latter.

An observation important for both proofs is that the above series exhibits absolute convergence, implying that its sum is independent of the order of the terms: it remains the same under any rearrangements of the series.

Proof 1

I group the successive pairs of terms with different signs:

$\begin{align}\displaystyle \pi-2&=1+\underbrace{\frac{1}{3}-\frac{1}{6}}\underbrace{-\frac{1}{10}+\frac{1}{15}}+\underbrace{\frac{1}{21}-\frac{1}{28}}\underbrace{-\frac{1}{36}+\frac{1}{45}}+\ldots\\ &=1+\frac{1}{6}-\frac{1}{30}+\frac{1}{84}-\frac{1}{180}-\ldots\\ &=1+\frac{4}{2\cdot 3\cdot 4}-\frac{4}{4\cdot 5\cdot 6}+\frac{4}{6\cdot 7\cdot 8}-\frac{4}{8\cdot 9\cdot 10}-\ldots, \end{align}$

which is exactly Nilakantha's series. The derivation is based on the following:

$\displaystyle\frac{2}{(n-1)n}-\frac{2}{n(n+1)}=\frac{4}{(n-1)\cdot n\cdot (n+1)}.$

Proof 2

The original proof by Jonas Castillo Toloza is much more involved but still depends on the series' absolute convergence. Regroup the terms into two series, with sums $A$ and $B,$ placing into each every other term:

$\displaystyle A=\frac{1}{1}-\frac{1}{6}+\frac{1}{15}-\frac{1}{28}+\frac{1}{45}-\ldots$

and

$\displaystyle B=\frac{1}{3}-\frac{1}{10}+\frac{1}{21}-\frac{1}{36}+\frac{1}{55}-\ldots$

Let's find $A$ first:

$\begin{align}\displaystyle A&=\frac{1}{1}-\frac{1}{6}+\frac{1}{15}-\frac{1}{28}+\frac{1}{45}-\ldots\\ &=\frac{2}{2}-\frac{2}{3\cdot 4}+\frac{2}{5\cdot 6}-\frac{2}{7\cdot 8}+\frac{2}{9\cdot 10}-\ldots\\ &=2\bigg(1-\frac{1}{2}\bigg)-2\bigg(\frac{1}{3}-\frac{1}{4}\bigg)+2\bigg(\frac{1}{5}-\frac{1}{6}\bigg)-2\bigg(\frac{1}{7}-\frac{1}{8}\bigg)+2\bigg(\frac{1}{9}-\frac{1}{10}\bigg)-\ldots\\ &=2\bigg(1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-\ldots\bigg)-2\bigg(\frac{1}{2}-\frac{1}{4}+\frac{1}{6}-\frac{1}{8}+\frac{1}{10}-\ldots\bigg)\\ &=2\cdot\frac{\pi}{4}-\bigg(\frac{1}{1}-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\ldots\bigg)\\ &=\frac{\pi}{2}-\ln 2, \end{align}$

the first being the Leibniz series, the second Taylor's formula for $\ln (1+x)$ at $x=1.$

We proceed similarly to compute $B$:

$\begin{align}\displaystyle B&=\frac{1}{3}-\frac{1}{10}+\frac{1}{21}-\frac{1}{36}+\frac{1}{55}-\ldots\\ &=\frac{2}{2\cdot 3}-\frac{2}{4\cdot 5}+\frac{2}{6\cdot 7}-\frac{2}{8\cdot 9}+\frac{2}{10\cdot 11}-\ldots\\ &=2\bigg(\frac{1}{2}-\frac{1}{3}\bigg)-2\bigg(\frac{1}{4}-\frac{1}{5}\bigg)+2\bigg(\frac{1}{6}-\frac{1}{7}\bigg)-2\bigg(\frac{1}{8}-\frac{1}{9}\bigg)+2\bigg(\frac{1}{10}-\frac{1}{11}\bigg)-\ldots\\ &=\bigg(1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\ldots\bigg)-2\bigg(\frac{1}{3}-\frac{1}{5}+\frac{1}{7}-\frac{1}{9}+\ldots\bigg)\\ &=\ln 2+2\bigg(\frac{\pi}{4}-1\bigg)=\ln 2+\frac{\pi}{2}-2. \end{align}$

Finally, $\displaystyle A+B=\bigg(\frac{\pi}{2}-\ln 2\bigg)+\bigg(\ln 2+\frac{\pi}{2}-2\bigg)=\pi -2.$

Acknowledgement: I've been consulting lifesmith.com for a treatment of the orginal proof which was rather hard to decipher.

Proof 3

The proof is by Grégoire Nicollier, University of Applied Sciences of Western Switzerland.

The proof is short, simple, and self-contained for $\displaystyle\pi-2=\sum_{n=2}^\infty\frac{(-1)^{1+\lfloor n/2\rfloor}}{\binom n2}\;$. Using Leibniz' formula for $\dfrac\pi4$ and $\dfrac1n-\dfrac1{n+1}=\dfrac1{n(n+1)}$ one obtains

$\displaystyle\begin{align} \pi-2 &= 4\left(1-\frac13+\frac15-\frac17+\cdots\right)-2\\ &= 2\left(1-\frac23+\frac25-\frac27+\cdots\right)\\ &= 2\left(1-\frac12+\frac12-\frac13-\frac13+\frac14-\frac14+\frac15+\frac15-\frac16+\frac16-\frac17-\cdots\right)\\ &= 2\left(\frac1{1\cdot2}+\frac1{2\cdot3}-\frac1{3\cdot4}-\frac1{4\cdot5}+\frac1{5\cdot6}+\frac1{6\cdot7}-\cdots\right). \end{align}$

Using now $\dfrac1{(n-1)n}-\dfrac1{n(n+1)}=\dfrac2{(n-1)\cdot n\cdot(n+1)}\;$ one has immediately Nilakantha's series and its version from another page.

Pi in Pascal's Triangle via Triangular Numbers

Pascal's Triangle and the Binomial Coefficients

71591391