e in the Pascal Triangle

Harlan Brothers has recently discovered the fundamental constant e hidden in the Pascal Triangle; this by taking products - instead of sums - of all elements in a row:

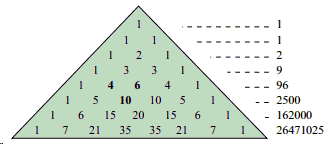
row products in Pascal Triangle

If \(s_n\) is the product of the terms in the \(n\)th row, then

\(\displaystyle \mbox{lim}_{n\rightarrow\infty} \frac{s_{n-1}s_{n+1}}{s_{n}^{2}} = e. \)

Proof

The terms in the \(n\)th row of the Pascal Triangle are the binomial coefficients \({n\choose k}\) so that

\(\displaystyle s_{n}=\prod_{k=0}^{n}{n\choose k}=\frac{(n!)^{n+1}}{\prod_{k=0}^{n}k!^{2}}. \)

This gives

\(\displaystyle \begin{align} \frac{s_{n+1}}{s_{n}} &= \frac{(n+1)!\space ^{n+2}}{(n!)^{n+1}}\cdot\frac{\prod_{k=0}^{n}k!^{2}}{\prod_{k=0}^{n+1}k!^{2}}\\\\ &= \frac{(n+1)^{n+2}n!}{1}\cdot\frac{1}{(n+1)!^{2}}\\\\ &= \frac{(n+1)^{n+1}}{(n+1)!}\\\\ &= \frac{(n+1)^{n}}{n!}. \end{align} \)

It follows that

\(\displaystyle \begin{align} \frac{s_{n+1}s_{n-1}}{s_{n}^2} &= \frac{(n+1)^n}{n!}\cdot\frac{(n-1)!}{n^{n-1}}\\\\ &= \bigg(\frac{n+1}{n}\bigg)^n\\\\ &= \bigg(1+\frac{1}{n}\bigg)^{n}. \end{align} \)

Which is a well known expression whose limit is \(e\).

References

H. J. Brothers, Pascal's triangle: The hidden stor-\(e\), The Mathematical Gazette, March 2012, 145
H. J. Brothers, Finding e in Pascal's triangle, Mathematics Magazine, 85, No. 1 (2012), 51

Pascal's Triangle and the Binomial Coefficients

71551956