Six Incircles in an Equilateral Triangle
What is it about?
A Mathematical Droodle

Explanation

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

The applet purports to illustrate one of the many properties of an equilateral triangle.

Let M be a point inside an equilateral triangle ABC, with pedal points A', B', and C', as shown. The lines joining M to the six points split the triangle into six smaller ones. Circles are inscribed into each of the latter.

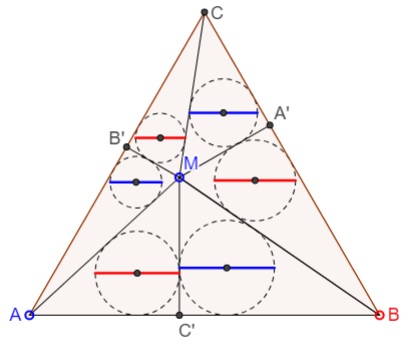
six incircles

If the diameter of the incircle of triangle UVW is denoted d(UVW), the applet suggests that

(1)

d(AMB') + d(BMC') + d(CMA') = d(A'MB) + d(B'MC) + d(C'MA).

For a proof, note that all six triangles are right, with the right angles at the pedal points A', B', C'. For a right triangle with legs a and b and the hypotenuse c, the inradius r is determined by

(2)

2r = a + b - c,

see the diagram in the Proof #33 of the Pythagorean proposition. With (2) in mind, (1) reduces to

(3)

AB' + BC' + CA' = A'B + B'C + C'A.

Draw AbAc||BC, BaBc||AC, and CaCb||AB. This gets us three equilateral triangles with the pedal points A', B', C' as the midpoints of their bases. That is to say,

(4)

A'Bc = A'Cb
B'Ca = B'Ac
C'Ab = C'Ba.

Substituting (4) into (3) and noting that, e.g., AB' = ACa + CaB', we get the following equivalent for (3)

(5)

ACa + BAb + CBc = BCb + CAc + ABa.

Finally observe that

(6)

ACa = BCb
BAb = CAc
CBc = ABa,

which proves (5).

References

  1. T. Andreescu, B. Enescu, Mathematical Olympiad Treasures, Birkhäuser, 2004

Related material
Read more...

  • A problem with equilateral triangles: an interactive illustration
  • Six Incircles in Equilateral Triangle
  • Equilateral Triangle, Straight Line and Tangent Circles
  • Equilateral Triangles on Diagonals of Antiequilic Quadrilateral
  • Equilateral Triangles On Sides of a Parallelogram
  • Equilateral Triangles On Sides of a Parallelogram II
  • Equilateral Triangles on Sides of a Parallelogram III
  • Triangle Classification
  • Equilateral Triangles and Incircles in a Square
  • Equal Areas in Equilateral Triangle
  • A Circle Rolling in an Equilateral Triangle
  • Viviani's Theorem
  • Regular Polygons in a Triangular Grid
  • Common Centroids Lead to Equilateral Triangle

    • |Activities| |Contact| |Front page| |Contents| |Geometry|

    Copyright © 1996-2018 Alexander Bogomolny

    72187123