Van Schooten's and Pompeiu's Theorems
What are these?
A Mathematical Droodle
3 November 2014, Created with GeoGebra
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
Van Schooten's and Pompeiu's Theorems
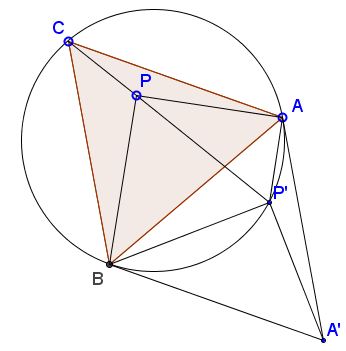
The applet illustrates two theorems discovered three hundred years apart. Let $P$ be a point in the plane of an equilateral $\Delta ABC.$ Both theorems are concerned with the relative lengths of the segments $AP,$ $BP,$ and $CP,$ joining $P$ the vertices of $\Delta ABC.$
Theorem (F. van Schooten, 1615 - 1660)
For $P$ on the circumcircle of $\Delta ABC.$ The longest of the three segments equals the sum of the shorter two.
Theorem (D. Pompeiu, 1873 - 1954)
For $P$ not on the circumcircle of $\Delta ABC,$ there exists a triangle with sides $PA,$ $PB,$ and $PC.$
(The triangle in question is known as Pompeiu's triangle.)
Ptolemy's theorem offers one approach to proving the theorems. A proof below is more elementary.
For a proof, rotate the plane $60^{\circ}$ around $B$ so as to make vertex $C$ overlap vertex $A.$ Let $A'$ and $P'$ be the images of $A$ and $P,$ respectively. I'll show that $APP'$ is Pompeiu's triangle.
By the construction, $\Delta BPP'$ is equilateral, so that $PP' = BP.$ In addition, $AP'$ is the image under the above rotation of $CP,$ so that $AP' = CP.$ The remaining side in $\Delta APP'$ is just $AP,$ and we are done with Pompeiu's theorem.
Assuming $A,$ $P,$ and $P'$ are collinear (i.e., when Pompeiu's triangle is degenerate), $\angle AP'B$ is either $60^{\circ}$ or $120^{\circ}.$ (This is because it is either equal to $\angle BPP',$ which is $60^{\circ},$ or is supplementary to it.) But then the quadrilateral $ABCP$ is cyclic, proving van Schooten's theorem and its converse.
Remark 1
Van Schooten's configuration appears in the following simple lemma:
Assume in $\Delta ABC$ $\angle BAC=120^{\circ}.$ Let $D$ be the foot of the angle bisector from $A.$ Then $\displaystyle AD=\frac{AB\cdot AC}{AB+AC}.$
For a proof, consider the circumcircle $(ABC)$ and let $E$ be the point where $AD$ crosses $(ABC).$ $E$ is the midpoint of the arc $BC$ opposite $A.$ This makes $\Delta BCE$ equilateral and the required proportion could be written as $\displaystyle AD=\frac{AB\cdot AC}{AE}$ (or, in the notations used for Pompeiu's theorem, $\displaystyle DP'=\frac{AP'\cdot BP'}{CP'},$ where $D$ is the intersection of $CP'$ and $AB.)$
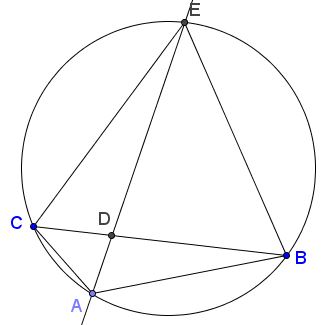
Triangles $CDE$ and $ADB$ are similar, so that $\displaystyle\frac{AD}{CD}=\frac{AB}{CE}.$ But $CE=BC,$ hence,
$\displaystyle AD=AB\frac{CD}{BC}.$
By a property of angle bisectors, $\displaystyle\frac{AB}{AC}=\frac{BD}{CD},$ implying
$\displaystyle\frac{AB+AC}{AC}=\frac{BD+CD}{CD}=\frac{BC}{CD}.$
Combining the two ratios yields $\displaystyle AD=AB\frac{AC}{AB+AC}=\frac{AB\cdot AC}{AB+AC}.$
Remark 2
van Schooten's theorem admits a non-trivial extension for triangles that are not equilateral!
(There is another proof.)
There is also a converse construction of finding an eqilateral triangle.
References
- T. Andreescu, R. Gelca, Mathematical Olympiad Challenges, Birkhäuser, 2004, p. 4.
Ptolemy's Theorem
- Ptolemy's Theorem
- Sine, Cosine, and Ptolemy's Theorem
- Useful Identities Among Complex Numbers
- Ptolemy on Hinges
- Thébault's Problem III
- Van Schooten's and Pompeiu's Theorems
- Ptolemy by Inversion
- Brahmagupta-Mahavira Identities
- Casey's Theorem
- Three Points Casey's Theorem
- Ptolemy via Cross-Ratio
- Ptolemy Theorem - Proof Without Word
- Carnot's Theorem from Ptolemy's Theorem
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581658
