Brahmagupta-Mahavira Identities
In a cyclic quadrilateral $ABCD$ with sides $a,$ $b,$ $c,$ $d,$ as shown, the diagonals can be computed via
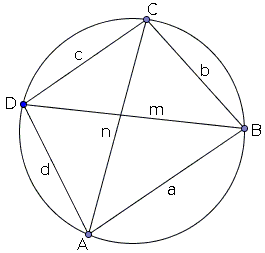
$\begin{align}\displaystyle m^{2} &= \frac{(ab + cd)(ac + bd)}{ad + bc}\\ n^{2} &= \frac{(ac + bd)(ad + bc)}{ab + cd}. \end{align}$
Most of the sources attribute this result to the great 9th century Indian mathematician Mahavira (or Mahaviracharya, meaning Mahavira the Teacher). However, according to Richard Askey with a reference to Henry Thomas Colebrooke the formulas have been known to another great Indian mathematician Brahmagupta already in the 7th century.
We have established these identities elsewhere in two ways. The gem of a proof that follows is due to yet another Indian mathematician Paramesvara who worked in the 15th century. This is really a beautiful
Proof
Ptolemy's formula in a cyclic quadrilateral tells us that
$n\cdot m = b\cdot d + a\cdot c.$
Let's interchange the sides $a$ and $d:$
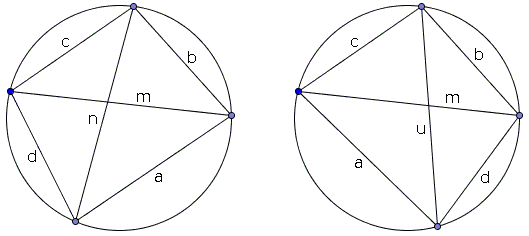
The operation will leave the quadrilateral cyclic and the diagonal $m$ unchanged. If the other diagonal is $u,$ the Ptolemy's formula gives,
$mu = a\cdot b + c\cdot d.$
Similarly, an exchange of $a$ and $b$ yields a cyclic quadrilateral with diagonals $u$ and $n;$ we have the identity:
$un = a\cdot d + b\cdot c.$
We get $m^{2}$ multiplying the first two and dividing by the third identity:
$\displaystyle m^{2} = \frac{(nm)(mu)}{un} = \frac{(b\cdot d + a\cdot c)(a\cdot b + c\cdot d)}{a\cdot d + b\cdot c}.$
For $n^{2},$ we have,
$\displaystyle n^{2} = \frac{(nm)(un)}{mu} = \frac{(b\cdot d + a\cdot c)(a\cdot d + b\cdot c)}{a\cdot b + c\cdot d}.$
And, for the ratio $\displaystyle\frac{m}{n},$ Ptolemy's second theorem
$\displaystyle\frac{m}{n} = \frac{a\cdot b + c\cdot d}{a\cdot d + b\cdot c}.$
References
- R. Askey, Completing Brahmagupta's Extension of Ptolemy's Theorem, in K. Alladi et al. (eds.), The Legacy of Alladi Ramakrishnan in the Mathematical Sciences, Springer Science+Business Media, LLC 2010
- H. T. Colebrooke, Algebra: With Arithmetic and Mensuration From The Sandskrit of Brahmagupta and Bhascara, 1817, reprinted, Kessinger, Whitefish, MT, USA,
- J. L. Heilbron, Geometry Civilized, Oxford University Press, Oxford, 2000, p. 219.
Ptolemy's Theorem
- Ptolemy's Theorem
- Sine, Cosine, and Ptolemy's Theorem
- Useful Identities Among Complex Numbers
- Ptolemy on Hinges
- Thébault's Problem III
- Van Schooten's and Pompeiu's Theorems
- Ptolemy by Inversion
- Brahmagupta-Mahavira Identities
- Casey's Theorem
- Three Points Casey's Theorem
- Ptolemy via Cross-Ratio
- Ptolemy Theorem - Proof Without Word
- Carnot's Theorem from Ptolemy's Theorem
|Contact| |Front page| |Contents| |Geometry| |Up|
Copyright © 1996-2018 Alexander Bogomolny
73599816
