Ptolemy Theorem - Proof Without Words

In a cyclic ABCD quadrilateral with sides a, b, c, d, and diagonals e and f, the product of diagonals equals the sum of the products of the opposite sides:

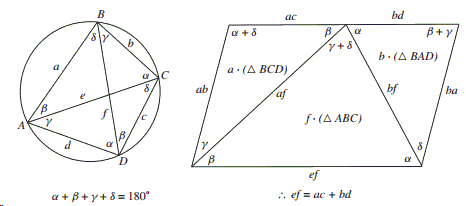
Ptolemy Theorem - proof without words

References

  1. W. Derrick, J. Herstein, Proof Without Words: Ptolemy's Theorem, The College Mathematics Journal, v 43, n 5, November 2012, p 386

Ptolemy's Theorem

  1. Ptolemy's Theorem
  2. Sine, Cosine, and Ptolemy's Theorem
  3. Useful Identities Among Complex Numbers
  4. Ptolemy on Hinges
  5. Thébault's Problem III
  6. Van Schooten's and Pompeiu's Theorems
  7. Ptolemy by Inversion
  8. Brahmagupta-Mahavira Identities
  9. Casey's Theorem
  10. Three Points Casey's Theorem
  11. Ptolemy via Cross-Ratio
  12. Ptolemy Theorem - Proof Without Word
  13. Carnot's Theorem from Ptolemy's Theorem

|Contact| |Front page| |Contents| |Geometry| |Up|

Copyright © 1996-2018 Alexander Bogomolny

70557284