Carnot's Theorem from Ptolemy's Theorem

Below I shall apply Ptolemy's theorem to derive a theorem due Lazare Carnot:

In any triangle $ABC,$ the (algebraic) sum of the distances (with suitable signs) from the circumcenter $O$ to the sides, is $R + r,$ the sum of the circumradius and the inradius:

$\pm OA' \pm OB' \pm OC' = R + r.$

The perpendiculars $OA'$, $OB'$, $OC'$ are preceded with the minus sign if their intersection with the interior of $\Delta ABC$ is not empty, and with a plus, otherwise.

We are going to obtain Carnot's theorem from that of Ptolemy which is usually comes in he following (or close) formulation:

For a quadrilateral inscribed in a circle, the sum of the products of the two pairs of opposite sides equals the product of its two diagonals.

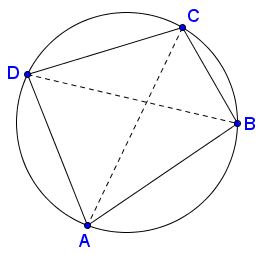
Ptolemy's theorem - common case

(1)

$BC\cdot AD+AB\cdot CD = AC\cdot BD.$

Implicit in this formulation is the requirement for the quadrilateral to be simple (no intersection of sides except for the vertices) and, hence, convex. Ptolemy's theorem applies only to simple inscribed quadrilateral. If that is not the case, the quadrilateral admits an alternative property.

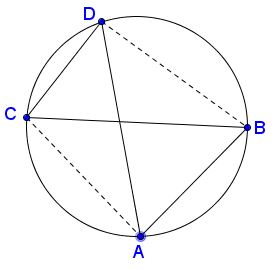
Ptolemy's theorem - negative signs case

For the above quadrilateral, omitting for a moment which of the segments are the diagonals and which its sides, we obtain

$AB\cdot CD+AC\cdot BD=AD\cdot BC,$

or,

(2)

$BC\cdot AD-AB\cdot CD=AC\cdot BD,$

which is practically the same as (1), except for the minus sign in front of the product of the non-intersecting sides.

Now for a proof of Carnot's theorem. $O,R,a,b,c,A',B',C'$ will denote the circumcenter, the circumradius, the lengths of the sides $BC,$ $AC,$ and $AB,$ and the feet of the perpendiculars from $O$ to those sides, respectively. $A',$ $B',$ $C'$ are the midpoints of the respective sides of $\Delta ABC.$ $[X]$ will denote the area of shape $X.$

The underlying idea of the proof is to consider the circles with diameters on the segments joining the circumcenter with the vertices. We have to consider three cases.

Proof of Carnot's theorem (acute triangle)

For an acute triangle the circumcenter $O$ is always located within the interior of the triangle. We may observe three cyclic quadrilaterals, $AB'OC',$ $BC'OA',$ and $CA'OB'.$ (Their circumcircles have $AO,$ $BO,$ $CO$ as diameters.)

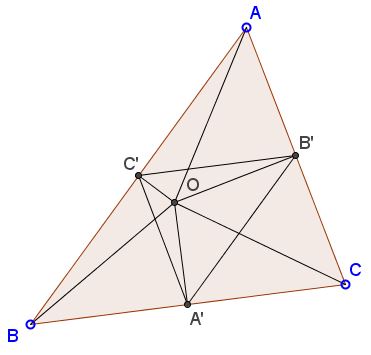
Ptolemy's theorem - acute triangle

Two each of these we apply Ptolemy's theorem (1). For example, in $AB'OC'$ we have

$AO\cdot B'C'= AB'\cdot OC'+AC'\cdot OB'.$

In other words, $\displaystyle AO\cdot \frac{a}{2}= \frac{b}{2}\cdot OC'+\frac{c}{2}\cdot OB'$ which after multiplying by $2$ becomes, $a\cdot R= b\cdot OC'+c\cdot OB'.$ Analogous identities hold for the other two quadrilaterals. In addition, there are two formulas for the area $[\Delta ABC]:$

$2[\Delta ABC]=a\cdot OA'+b\cdot OB'+c\cdot OC'$ and
$2[\Delta ABC]=r(a+b+c),$

where $r$ is the inradius of $\Delta ABC.$ Let's right these all together:

$\begin{align} a\cdot R &= b\cdot OC'+c\cdot OB'\\ b\cdot R &= c\cdot OA'+a\cdot OC'\\ a\cdot R &= a\cdot OB'+b\cdot OA'\\ 2[\Delta ABC] &=a\cdot OA'+b\cdot OB'+c\cdot OC'\\ r(a+b+c) &= 2[\Delta ABC]. \end{align}$

Summing up results in $(R+r)(a+b+c)=(OA'+OB'+OC')(a+b+c),$ i.e., $R+r=OA'+OB'+OC',$ Lazare Carnot's theorem.

Proof of Carnot's theorem (obtuse triangle)

In case of an obtuse triangles we'll replace (1) with (2) and modify one of the area formulas.

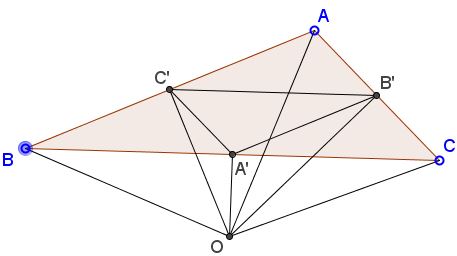
Ptolemy's theorem - obtuse triangle

For example, if the angle at $A$ is obtuse, we have

$\begin{align} a\cdot R &= b\cdot OC'+c\cdot OB'\\ b\cdot R &= a\cdot OC'-c\cdot OA'\\ a\cdot R &= a\cdot OB'-b\cdot OA'\\ 2[\Delta ABC] &=-a\cdot OA'+b\cdot OB'+c\cdot OC'\\ r(a+b+c) &= 2[\Delta ABC]. \end{align}$

Summing up results in $(R+r)(a+b+c)=(-OA'+OB'+OC')(a+b+c),$ i.e., $R+r=-OA'+OB'+OC',$ Lazare Carnot's theorem in this case.

Proof of Carnot's theorem (right triangle)

In case of a right triangle, Ptolemy's theorem reduces to the Pythagorean theorem. The circumcenter coincides with the midpoint of the hypotenuse ($A'$ in the diagram below):

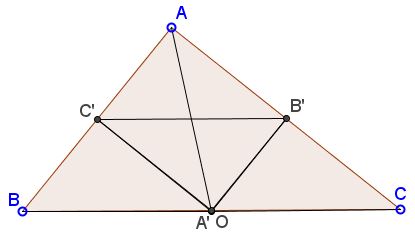
Ptolemy's theorem - right triangle

In this case, $R=\frac{1}{2}c,$ $r=\frac{1}{2}(a+b-c)$ and Carnot's theorem $R+r=OA'+OB'+OC'$ is immediate, with $OA'=0.$ The challenge of deducing this from the Pythagorean theorem is left as an exercise

Acknowledgment

The above is a little expanded version of a note Lazar Karno's Theorem by Abbas Rouhol Amini (Mathematical Spectrum, v 47 2014/2015 n 1, 41-42).

Ptolemy's Theorem

71950059