Equilateral Triangles On Sides of a Parallelogram
What Is It About?
A Mathematical Droodle
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
Equilateral Triangles On Sides of a Parallelogram
The applet suggests the following theorem [Honsberger, pp. 278-279]:
On the sides of a parallelogram $ABCD,$ construct similarly oriented equilateral triangles $ABX,$ $BCY,$ $CDZ,$ and $DAW.$ Not accidentally, the quadrilateral XYZW happens to be a parallelogram. On its sides, in turn, construct equilateral triangles $XYP,$ $YZQ$, $ZWR$, $WXS$ with the orientation opposite to that of $ABX,$ $BCY,$ $CDZ,$ and $DAW.$ Not surprisingly $PQRS$ is again a parallelogram. Surprisingly, $PQRS$ and $ABCD$ coincide.
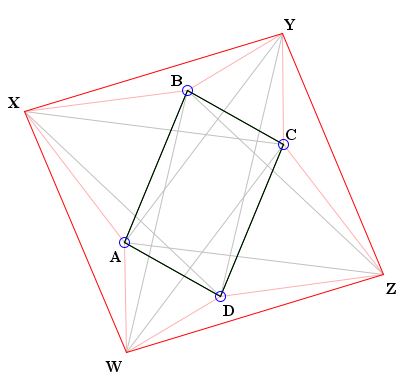
As on several other occasions (e.g., Three Isosceles Triangles, When a Triangle is Equilateral?, and others), we can make a good use of complex numbers. Points $X, Y, Z, W$ are linear combinations of $A, B, C, D$ with complex coefficients:
(1)
$\begin{align} X = cA + (1 - c)B,\\ Y = cB + (1 - c)C,\\ Z = cC + (1 - c)D,\\ W = cD + (1 - c)A,\\ \end{align}$
where
$c = (1 + i\sqrt{3})/2,\\ 1 - c = (1 - i\sqrt{3})/2.$
On the other hand, by construction,
$\begin{align} P &= cY + (1 - c)X,\\ Q &= cZ + (1 - c)Y,\\ R &= cW + (1 - c)Z,\\ S &= cX + (1 - c)W. \end{align}$
In terms of $A, B, C, D$ these can be written as
(2)
$\begin{align} P&= ((1 - c)^{2} + c^{2})B + c(1 - c)A + c(1 - c)C\\ &= A - B + C, \space\mbox{and similarly}\\ Q&= B - C + D,\\ R&= C - D + A,\\ S&= D - A + B.\\ \end{align}$
However, since $ABCD$ is a parallelogram, $A - B = D - C,$ so that, from the first identity in (2),
$\begin{align} P&= A - B + C\\ &= D - C + C\\ &= D, \end{align}$
and similarly for the other three vertices.
References
- Honsberger, In Pólya's Footsteps, MAA, 1999
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73583489
