Equivalence Relations

Equivalence relations permeate mathematics with several salient examples readily available:

Residue classes [a]_N consist of all numbers congruent (equivalent) modulo N
a negative number is a set of all equivalent pairs (a, b) of integers with a < b, where two pairs (a, b) and (c, d) belong to the same set (equivalence class) iff a + d = b + c
a rational number is a set of all equivalent pairs (a, b) of integers, where two pairs (a, b) and (c, d) are equivalent iff ad = bc
an irrational number is an equivalence class of sequences r₁, r₂, r₃, ... of rational numbers, where two sequences {r_i} and {s_i} are equivalent iff they there difference converges {r_i - s_i} to 0 as i→∞.

Examples are many and one may be inclined to think that the reason I do not cite more is that the level of abstraction of such examples rises so quickly as to make them incomprehensible to a casual reader. This is quite possible. Why make it difficult? However, I'd like to give one additional example. What's really interesting about it is that every one knows about it, learns it starting, say, at the age of 5, uses it virtually every minute. As a matter of fact, you came across it as you were reading the previous sentence.

What is this equivalence relation? This ubiquitous abstraction is the notion of integer as used in counting. Assume, in a foreign country whose language you do not speak (and starving for this reason), you ran into a McDonald's. You rush in but even in a foreign country not all of them are geniuses. The fellow there appears to react correctly to the word "hamburger" but you do not know how to say 5. What do you do? I bet you'll raise an open hand and turn the palm towards the fellow so that she'll see all your spread fingers clearly. And the fellow, an unlikely genius, will understand you perfectly well. Unlike a mathematical concept, this one is not strictly defined, but is used so universally we forget what counting and numbers are about.

Somehow, by the age of five, we know that

is equivalent to

while

is not equivalent to

But then again

is equivalent to

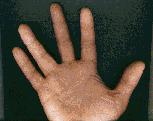
You can put it in many different ways. For example, you can say that

5 is a common something that five bear cubs and five sea otters got but six otters did not. (The something at hand is often called the property of fiveness.)
5 is what some sets have in common with the number of fingers on my hand
5 is the set of all sets that could be put into a 1-1 correspondence with the set of fingers on the picture above and to the right
5 is the set of all sets that are equivalent to the set of fingers on my hand, where two sets are called equivalent when a 1-1 correspondence exists between their elements

Mathematicians prefer the last two definitions. The last one enables me to point out how omnipresent equivalence relations actually are. People invent symbols (known as words) to denote some objects. Mathematicians also invent words, but, in addition, they attempt to explain the meaning they input to the word. They try to make it intuitive. They achieve this by distilling common usage into a simple, intuitive abstraction. Compare:

What's a cow? Here what Webster's New Collegiate Dictionary says:		Equivalence relation is a binary (in the sense that it relates two elements) relation that satisfies the following three properties:
1. the mature female of cattle (genus Bos) or of any animal the male of which is called bull (as the moose) 2. a domestic bovine animal regardless of sex or age		Reflexivity: a∼a (A set compares to itself) Symmetry: If a∼b then b∼a (If a set has as many elements as another set then the second set has as many elements as the first) Transitivity: If a∼b and b∼c then a∼c (If a set has as many elements as another set and this, in turn, has the same number of elements as a third set, then the first and the third are also equivalent)

Now you know that when you call somebody a cow the age does not count (although, why would you be talking to a cow?) On the other hand, if it came to your needing to look up the word cow in the first place, do you have a notion of what cattle, bovine, genus, moose are? Can you be sure that Bos is not a typo and the word Boss has been actually meant?

In math you may want to ask why these three properties have been selected to represent equivalence between sets? If you are indeed curious, try to think of other properties common to all equivalence relations you may think of. I can only offer a very lame excuse: over many-many years mathematicians agreed that the above three are the simplest and the commonest.

An important fact about equivalence relations is expressed by the following

Theorem

Let ∼ be an equivalence relation defined between elements of a set A. Then the set A can be written as a union ∪A_t of pairwise disjoint subsets A_t ⊂ A such that

a∼b iff there exists A_t such that a∈A_t and b∈A_t.

There are several ways to express the fact that a ∼ b. For example:

a is equivalent to b.
a and b are equivalent.
a and b belong to the same equivalence class.

40585918