A Possibly First Proof of the Concurrence of Altitudes
This is a matter of real wonderment that the fact of the concurrency of altitudes is not mentioned in either Euclid's Elements or subsequent writings of the Greek scholars. The timing of the first proof is still an open question; it is believed, though, that even the great Gauss saw it necessary to prove the fact. The earliest known proof was given by William Chapple (1718-1781) in 1749.
The discussion as to the precedence of the published proofs was quite heated. Following is an excerpt from a 1850 article by Thomas Stephens Davies in The Philosophical Magazine:
|
It is often extremely difficult to decide respecting originality in elementary investigations; for no one can undertake to look carefully through every elementary book that has been published, to ascertain whether some particular and simple proposition might not possibly be contained in it. Nevertheless some general criteria might be laid down, which would contribute towards probability on one side or another in most cases; and this presumed probability would often limit the trouble of the search to very narrow bounds. Almost every proposition naturally refers itself to a class; and if once observed, others of that class must soon follow. If, then, upon observing such a proposition we find it isolated, it is highly probable that it originated with the author who there gave it, or at least not long before. In the few cases which I have had occasion to examine minutely and carefully, I have rarely found this rule to fail--indeed, in no one to signally fail. This, too, is precisely the same in respect to analytical devices--and not widely different is the testimony of the history of experimental science.
This remark is made in consequence of a property of the triangle, now universally known, which appears to have been first given in an elementary treatise by Emerson (Geom., B. ii. pr. 32, 1763). "The perpendiculars from the angular points of a triangle to the opposite sides, pass through the same point." The property was, however, enunciated by Mr. Thomas Moss, an exciseman and able geometer, in 1751; and two neat demonstrations given to it shortly after by a writer who signs ΣΟΦΟΣ (probably Simpson), and by Edward Rollinson, in Turner's Mathematical Exercises. A property still more general had been given four or five years previously in the Mathematician, edited by Rollinson. The less general property was not, however, perceived to be deducible from the more general one, and both passed without further remark than the mere solutions till attention was called to the system connected inquiries in the Mathematical Repository (vol. vi), under one aspect; and under another in the Phil. Mag., vol. ii, p. 26, 2nd Ser., and the appendix to the Ladies' Diary, 1835. It may seem strange that so simple a property, and so many others similar or related to it, should have been unobserved by the ancients, and by their earlier followers after the revival of letters. It must be recollected, however, that the Greek geometers only valued a theorem (or even a Porism) except so far as it contributed to the solution of a problem. There are no traces, not even intimations, of their having regularly attempted to form classed collections of theorems, or to arrange systematically the many beautiful series of properties of figures that could not fail to have presented themselves during the solution of problems. Such properties were only selected as would be actually required in demonstrating the constructions of the cases of a problem. Of these the seventh book of Pappus is a collection of instances. The properties of αρβηλοσ given by him, form almost the only marked exception--or perhaps also Euclid's Porisms. We find at all events, extremely (if anything, properly speaking) concerning lines meeting in a point, or points ranging in a straight line. The modern French geometers were the first to enter upon this class of researches with any degree of system; and the results have justified their expectations, however sanguine. We need not then, after all, feel much surprise at finding the proposition in question claiming so recent a place in geometry; and the same may be said of a great number of now-familiar truths. Postscript, August 24.--Whilst reading the proof sheets, the Mechanics' Magazine of this date reached me, containing one of Mr. Wilkinson's able and elaborate analysis of our English mathematical periodicals, viz., of the Miscellanea Curiosa Mathematica, 1745-53, edited by Holliday, whose name has been already mentioned. As there is one passage which renders a slight modification of the preceding paragraph necessary, I quote it as it stands--from its offering less trouble, both to myself and the printer at the last moment, than recomposition and resetting would do. Speaking of art. xxxix., "A new Proposition in Geometry demonstrated by Mr. William Chapple, " he says:--
|
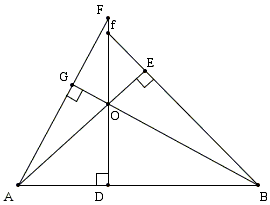
William Chapple's demonstration refers to the following diagram:
|
I reproduce W. Chapple's note verbatim:
|
SIR: Yours, etc. W. Chapple
PROPOSITION In any acute-angled triangle, if perpendiculars be let fall from each angle on the opposite side, they will all three intersect each other in one and the same point within the triangle. DEMONSTRATION In any obtuse-angled triangle, AOB, produce the sides AO and BO to E and G, and let fall the perpendiculars BE, AG, DO, and continue AG and DO till they intersect in F; then will BE, if continued, also intersect them in F, if the proportions be true; however let us, for the present, suppose it otherwise, and that it intersect OF in some point, as f, so that EF (not EF) be perpendicular to OE. Now 'tis plain that the triangles ABE, ADO, and OEf, are similar, as are also the triangles ABG, DBO, and OGF, and the triangles BOE, and AOG. Put |
Ackowledgement
I am grateful to FC for supplying me with the excerpts from the old magazines.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73573972
