All About Altitudes
In a triangle, an altitude is a segment of the line through a vertex perpendicular to the opposite side. An altitude is the portion of the line between the vertex and the foot of the perpendicular. Using the standard notations, in $\Delta ABC$, there are three altitudes: $AH_{a},$ $BH_{b},$ $CH_{c},$ where $H_a,$ $H_b,$ and $H_c$ are the feet of the perpendiculars on $BC,$ $AC,$ $AB$ (or their extensions) from the opposite vertices. The three lines meet at a point - the orthocenter of the triangle, which is usually denoted $H$.

There are many proofs of the existence of the orthocenter. A collection of about two dozens of such proofs can be found on a separate page. The feet of the altitudes lie in pairs on three circles with the sides of $\Delta ABC$ as diameters, e.g., $H_b$ and $H_c$ lie on circle $(BC):$
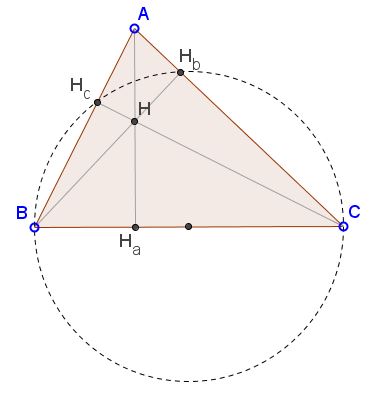
Applying the Intersecting Chords theorem in this configuration we obtain the following identities:
(1)
$AH\cdot HH_{a} = BH\cdot HH_{b} = CH\cdot HH_{c}.$
The reflections of $H'_b$ and $H'_c$ of $H_b$ and $H_c$ in the diameter also lie on circle $(BC):$
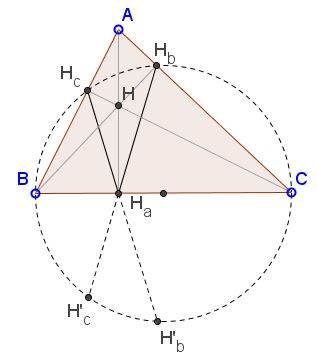
Thus, another application of the Intersecting Chords theorem gives
(2)
$BH_{a}\cdot CH_{a} = H_{a}H_{b}\cdot H_{a}H'_{c} = H_{a}H_{b}\cdot H_{a}H_{c}.$
By analogy, also $AH_{b}\cdot CH_{b} = H_{b}H_{a}\cdot H_{b}H_{c}$ and $AH_{c}\cdot BH_{c} = H_{c}H_{a}\cdot H_{c}H_{b}.$
There is another triple of circles with diameters on $AH,$ $BH,$ $CH:$
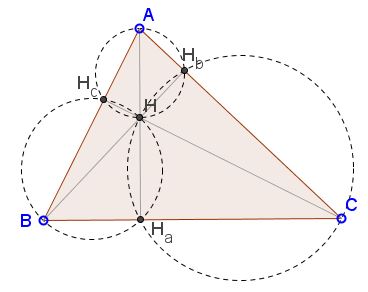
From this we conclude that
(3)
$\begin{align} AH_{c}\cdot AB &=AH_{b}\cdot AC,\\ BH_{a}\cdot BC &=BH_{c}\cdot BA,\\ CH_{b}\cdot CA &=CH_{a}\cdot CB. \end{align}$
Tran Quang Hung has observed that (2) and (3) combine to give
$\displaystyle\frac{1}{H_{a}H_{b}\cdot H_{a}H_{c}}=\frac{1}{BH_{c}\cdot BA}+\frac{1}{CH_{b}\cdot CA}.$
which, for a right triangle with the angle at $A$ $90^{\circ},$ leads to a well-known identity:
$\displaystyle\frac{1}{AH^{2}_{a}}=\frac{1}{AB^2}+\frac{1}{AC^2}.$
The altitudes possess a remarkable mirror property, e.g.,
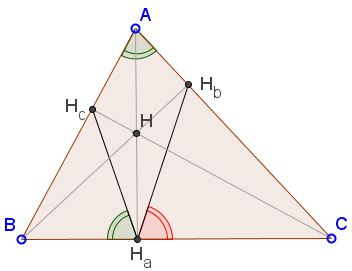
which, in particular, tells us that the sides of the orthic triangle $H_{a}H_{b}H_{c}$ are antiparallel in $\Delta ABC:$

The circumcircle $(H_{a}H_{b}H_{c})$ of the orthic triangle passes through the midpoints of the sides and the midpoints of the segments $AH,$ $BH,$ $CH,$ for which reason it is known as the 9-point circle.
The altitudes also appear in several metric relations between the elements of $\Delta ABC.$
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73571200
