A Triangle out of Three Broken Sticks
Problem

Solution, Part 1
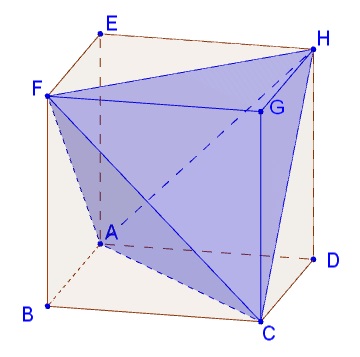
Assume the sticks are of length $1$ and consider the cube with vertices $A(0,0,0),$ $B(1,0,0),$ $D(0,1,0),$ $E(0,0,1),$ $C(1,1,0),$ $F(1,0,1),$ $H(0,1,1),$ and $G(1,1,1).$
The left pieces of the sticks are defined by their right points and I shall describe their lengths with the real $x,y,z\in(0,1).$ Thus the cube constitutes the sample space for all possible combinations of the breaking points. For $x,y,z$ to form a triangle, we need three inequalities:
$\begin{align} z&\lt x+y\\ y&\lt x+z\\ x&\lt y+z. \end{align}$
Note that, say, line $AF$ has the equation $z=x$ and line $AH$ the equation $z=y,$ so that the plane through $A,F,H$ is described by $z=x+y.$ The plane divides the space into two half-spaces. In the one that contains $G,$ $x+y\gt z.$
Similarly, the plane $AFC$ is described by $x=y+z$ and the plane $ACH$ by $y=x+z.$ The set of points that satisfies the three inequalities belongs to the intersection of the three half-spaces and the cube: that's the figure $V=ACFHG.$ It consists of two pyramids with the base $CFH$ and apices at $A$ and $G.$
$V$ is obtained from the cube by cutting corner pyramids $ACFB,$ $ACHD,$ and $AFHE.$ Each of these has volume $\displaystyle \frac{1}{3}\cdot\frac{1}{2}\cdot 1=\frac{1}{6}.$ It follows that the volume of $V$ is $\displaystyle 1-3\cdot\frac{1}{6}=\frac{1}{2}.$
Solution, Part 2
If now $x,y,z$ stand for the lengths of the longest pieces than $\displaystyle \frac{1}{2}\lt x,y,z\lt 1.$ Then for example, $\displaystyle x+y\gt\frac{1}{2}+\frac{1}{2}=1\gt z,$ and, similarly, for the other two inequalities. We conclude that the probability in this case is $1.$
Solution, Part 3
If now $x,y,z$ stand for the lengths of shortest pieces then $0\lt x,y,z\lt\frac{1}{2}$ and each of the three is drawn uniformly randomly from the interval $\displaystyle\left(0,\frac{1}{2}\right).$ The situation is similar to Part 1 so that the probability in this case is $\displaystyle \frac{1}{2}.$
Solution, Part 4
First I should mention that quite a few people observed that in Part 1 whether we choose left or right pieces because both side lengths of a broken stick have the same probability distribution. This implies that when a random choice is made between the left and right pieces for each stick, the probability of getting a triangle is no different than in Part 1, i.e., $\displaystyle \frac{1}{2}.$
It occurred to me that there might be a difference with the case where the choice is made between the long and the short pieces, rather than between the left and the right ones. Many people insisted their should not be any difference. I made a mistake of thinking that since $\min(x,1-x)$ is distributed on $\displaystyle \left[0,\frac{1}{2}\right]$ while $\max(x,1-x)$ is distributed on $\displaystyle \left[\frac{1}{2},1\right].$ Tangentially, support also came from the difference in probabilities in Parts 2 and 3. That was explained and corrected by Timon Klugge.
where the three numbers $x,y,z$ satisfied $0\le x,y,z\le\frac{1}{2}$ and formed a triangle. Let $\Delta(x,y,z)=1,$ if $x,y,z$ form a triangle, and $0,$ otherwise. We could denote the probability we found as$\displaystyle P\left(\Delta(x,y,z)=1\,|\,0\le x,y,z\le\frac{1}{2}\right)=\frac{1}{2}.$
Now, if $\Delta(x,y,z)=1$ then also $\Delta(2x,2y,2z)=1,$ such that we were able to conclude that in the domain of definition, $[0,1]^3,$ $\Delta(x,y,z)=1$ half the time.
Now, there is a harder road to arrive at the same conclusion. Assume $\displaystyle 0\le x,y,z\le\frac{1}{2},$ what is the probability of $P(\Delta(x,y,z)=1)?$ In other words, what is $\displaystyle P\left(\Delta(x,y,z)=1\text{ and }0\le x,y,z\le\frac{1}{2}\right)?$ The formula for conditional probability gives
$\displaystyle\begin{align}&P\left(\Delta(x,y,z)=1\text{ and }0\le x,y,z\le\frac{1}{2}\right)\\ &\qquad= P\left(\Delta(x,y,z)=1)\,|\,0\le x,y,z\le\frac{1}{2}\right)\cdot P\left(0\le x,y,z\le\frac{1}{2}\right)\\ &\qquad=\frac{1}{2}\cdot\frac{1}{8}=\frac{1}{16}. \end{align}$
Similarly, with the result of Part 2, we conclude that
$\displaystyle\begin{align}&P\left(\Delta(x,y,z)=1\text{ and }\frac{1}{2}\le x,y,z\le 1\right)\\ &\qquad= P\left(\Delta(x,y,z)=1)\,|\,\frac{1}{2}\le x,y,z\le 1\right)\cdot P\left(\frac{1}{2}\le x,y,z\le 1\right)\\ &\qquad=1\cdot\frac{1}{8}=\frac{1}{8}. \end{align}$
Now we have to consider six additional case that come in two groups of three. If $S,L$ stand for "short" and long, respectively and define $S_x=\min(x,1-x)$ and $L_x=\max(x,1-x),$ and similarly for $y$ and $z$ then there are eight combinations $SSS,$ $SSL,$ ..., $LLL.$ The first, $SSS,$ and the last, $LLL,$ have been just treated.
We need to find $P(\Delta(x,y,z)=1\,|\,SSL)$ and then also $P(\Delta(x,y,z)=1\,|\,SLL).$
SSL
We have three variables $x,y,z$ that satisfy
$\displaystyle \begin{align} x&\lt\frac{1}{2}\\ y&\lt\frac{1}{2}\\ z&\gt\frac{1}{2} \end{align}$
that, in addition, need to satisfy, $x+y\gt z.$ Points $(x,y,z)$ that satisfy the four conditions are located inside the corner pyramid in a small cube:
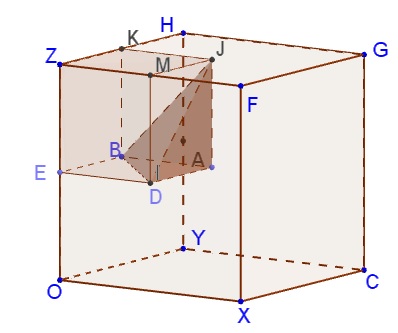
The volume of this pyramid, relative to the larger cube is $\displaystyle \frac{1}{8}\cdot\frac{1}{6}=\frac{1}{48}.$ Cycling through the three variables gives $\displaystyle 3\cdot\frac{1}{48}=\frac{1}{16}.$
SLL
In this case we need to satisfy the following inequalities:
$\displaystyle \begin{align} x&\lt\frac{1}{2}\\ y&\gt\frac{1}{2}\\ z&\gt\frac{1}{2}\\ x+y&\gt z\\ x+z&\gt y. \end{align}$
The points $(x,y,z)$ that satisfy all five inequalities lie outside two pyramids in the small cube:
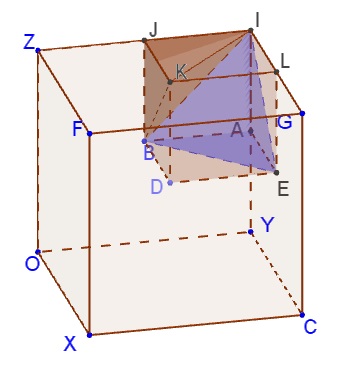
The relative volume of that space is $\displaystyle \frac{1}{8}\left(1-2\cdot\frac{1}{6}\right)=\frac{1}{12}.$ Cycling through the three variables gives $\displaystyle 3\cdot\frac{1}{12}=\frac{1}{4}.$ Putting everything together, denote $\mathcal{S}=\{SSS, SSL,\ldots, SSS\},$ then, the formula of total probability,
$\displaystyle\begin{align}P(\Delta(x,y,z)=1)&=\sum_{\omega\in\mathcal{S}}P(\Delta)x,y,z)=1\,|\,\omega)\\ &=\frac{1}{16}+\frac{1}{16}+\frac{1}{4}+\frac{1}{8}\\ &=\frac{1}{2}. \end{align}$
As Long Huynh Huu has observed that was clear to start with.
Solution, Part 5
The expectation that $x,y,z\in(0,1)$ form side lengths of a triangle is $\displaystyle E_{x,y,z}=0\cdot\frac{1}{2}+1\cdot\frac{1}{2}.$
The same is true if we replace $x$ with $1-x,$ $y$ with $1-y,$ or $z$ with $1-z.$ There are eight such combinations. The eight events are not mutually exclusive (explaining the difficulty with Part 4), however the individual expectations can be summed up, giving the total expectation of $\displaystyle 8\cdot \frac{1}{2}=4.$
Solution 2
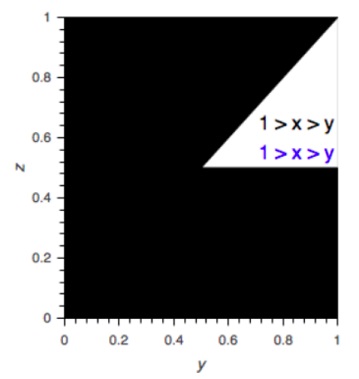
WLOG, let the length of the sticks be unity. Let the length of the three pieces (sorted) be $x\geq y\geq z$. Let the regions in the $X,Y,Z$ space (and the projections of the space) where the sorting holds and where forming a triangle is possible be termed "feasible region" and "positive region", respectively.
Left Pieces
The figure below shows the feasible region in the $YZ$ plane in white with the conditions on $x$. The conditions in black and blue are for the positive and feasible regions, respectively.
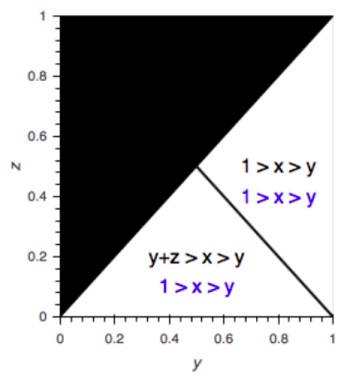
The probability of triangulation is given by
$\displaystyle \begin{align} P&=\frac{\int_{z=0}^{1/2}\int_{y=z}^{1-z}\int_{x=y}^{y+z}dxdydz + \int_{y=1/2}^{1}\int_{z=1-y}^{y}\int_{x=y}^{1} dxdzdy} {\int_{z=0}^{1/2}\int_{y=z}^{1-z}\int_{x=y}^{1}dxdydz + \int_{y=1/2}^{1}\int_{z=1-y}^{y}\int_{x=y}^{1} dxdzdy} \\ &=\frac{1/24+1/24}{1/8+1/24}=1/2. \end{align}$
Longer Pieces
The figure below corresponds to this case. Clearly, the probability is $1$ in this case.
Shorter Pieces
This case is same as the "left pieces" except that $x$, $y$, and $z$ are drawn from $(0,0.5]$ instead of $(0,1.0)$. The probability does not change by this scaling and the probability is $1/2$.
Random Chioce
For the case of "left pieces", the length of the stick has a uniform distribution of $(0,1)$. Choosing one side or the other does not change the distribution for the chosen stick as both sides are identically distributed. Thus, the probability for this case remaines $1/2$.
Expected Number of Triangles
There are $8$ combinations depending on which side is chosen for each stick. For each combination, the chosen side for a stick can be arbitrarily labelled "left". This approach maps every combination to the "left pieces" case and the probability of forming a triangle is $1/2$. Thus, the expected number of triangles is $4$.
Acknowledgment
This is an extension of problem 96 (in my Russian edition) from Challenging Mathematical Problems With Elementary Solutions by A. M. Yaglom and I. M. Yaglom.
- Inequalities in Triangle
- Padoa's Inequality
$(abc\ge (a+b-c)(b+c-a)(c+a-b))$
- Refinement of Padoa's Inequality $\left(\displaystyle \prod_{cycl}(a+b-c)\le 2\min_{cycl}\{a\cdot\frac{b^2c^2}{b^2+c^2}\}\le 2\max_{cycl}\{a\cdot\frac{b^2c^2}{b^2+c^2}\}\le abc\right)$
- Erdos-Mordell Inequality $(OA+OB+OC\ge 2(OP+OQ+OR) )$
- From Triangle Inequality to Inequality in Triangle $(\max\{A,B,C,D,E,F\}\le a^ab^bc^c)$
- Area Inequalities in Triangle $([\Delta NAP]\le\frac{1}{4}[\Delta ABC])$
- Area Inequality in Three Triangles $\displaystyle 2(\sqrt{S_1}+\sqrt{S_2}+\sqrt{S_3})^2 \lt \sum_{cycl}a_1^2 + \sum_{cycl}a_2^2 + \sum_{cycl}a_3^2.$
- Area Inequality in Triangle II $([PBF]\le\frac{1}{6})$
- An Inequality in Triangle $(a^3b+b^3c+c^3a-a^2b^2-b^2c^2-c^2a^2\ge 0)$
- An Inequality in Triangle, II $(m_al_a+m_bl_b+m_cl_c\ge p^2)$
- An Inequality in Triangle III $\displaystyle\left(\frac{a(b+c)}{bc\cdot\cos^2\frac{A}{2}}+\frac{b(c+a)}{ca\cdot\cos^2\frac{B}{2}}+\frac{c(a+b)}{ab\cdot\cos^2\frac{C}{2}}\ge 8\right)$
- An Inequality in Triangle IV $\left(\begin{align}\sqrt{2}&\left[\sqrt{p(p-a)}+\sqrt{p(p-b)}+\sqrt{p(p-c)}\right]\\ &\le\sqrt{p^2-m_a^2}+\sqrt{p^2-m_b^2}+\sqrt{p^2-m_c^2}, \end{align}\right)$
- An Inequality in Triangle, V $(m_am_bm_c\ge r_ar_br_c)$
- An Inequality in Triangle, VI $\displaystyle\left(\frac{h_a\cdot h_b}{h_a+h_b}\right)\lt h_c\left(\frac{h_a\cdot h_b}{|h_a-h_b|}\right)$
- An Inequality in Triangle, VII $\displaystyle\left(\left(\sum_{cycl}\frac{m_a^2}{m_b^2}\right)\left(\sum_{cycl}x^2\right)+2\left(\sum_{cycl}\frac{m_a}{m_c}\right)\left(\sum_{cycl}xy\right)\ge 0\right)$
- An Inequality in Triangle, VIII $\displaystyle\left(\sum_{cycl}\frac{5a^2-b^2-c^2}{\sqrt{m_bm_c}}\le 4\sum_{cycl}m_a\right)$
- An Inequality in Triangle, IX $\displaystyle\left( 27\prod_{cycl}IA'\cdot HA''\le\frac{1}{27}\prod_{cycl}\ell_ah_a\right)$
- An Inequality in Triangle, X $\displaystyle\left(\frac{1}{r^2}\sum_{cycl}a^3\cos B\cos C\ge 16\left(\sum_{cycl}\sin A\right)\left(\sum_{cycl}\cos^2 A\right)\right)$
- An Inequality in Triangle XI $\left(3(a^2+b^2+c^2)\lt 4(am_c+bm_a+cm_b)\right)$
- Inequality In Triangle: Sides and Angle Bisectors $\left(\displaystyle a+b+c \ge \frac{2\sqrt{3}}{3}(l_a+l_b+l_c)\right)$
- Weitzenböck's inequality
$(a^2 + b^2 + c^2 \ge 4\sqrt{3}S)$
- Two Refinements of the Ionescu-Weitzenbock Inequality $(a^2+b^2+c^2\ge 2\sqrt{3}\max\{am_a,bm_b,cm_c\})$
- Another Refinement of the Ionescu-Weitzenbock Inequality $(\displaystyle a^2+b^2+c^2-4\sqrt{3}S\ge 2\sqrt{3}(m_a^2-h_a^2))$
- Early Refinement of the Ionescu-Weitzenbock Inequality $(\displaystyle a^2+b^2+c^2-(a-b)^2-(b-c)^2-(c-a)^2\ge 4\sqrt{3}S)$
- Weitzenbock by Sanchez $([ABC](1+\sqrt{3}]\le [ANBMCP])$
- An Inequality In Triangle That Involves the Four Basic Centers $\left(\displaystyle \sum_{cycl}(AH+2\cdot AI+3\cdot AO+4\cdot AG)\ge 60r\right)$
- An Inequality in Acute Triangle, Courtesy of Ceva's Theorem $\displaystyle\left(AB'\cdot BC'\cdot CA'+AB''\cdot BC''\cdot CA''+AB'''\cdot BC'''\cdot CA'''\le \frac{3}{8}abc\right)$
- Problem 4020 from Crux Mathematicorum $([MNP] \le [DEF])$
- A Two-Triangle Inequality $(a^2(-a'^2+b'^2+c'^2)+b^2(a'^2-b'^2+c'^2)+c^2(a'^2+b'^2-c'^2)\ge 16KK')$
- A Two-Triangle Inequality II $\left(\displaystyle\frac{a+b+c}{3\sqrt{3}R}\le\frac{\displaystyle\cos\frac{A}{2}+\cos\frac{B}{2}+\cos\frac{C}{2}}{\displaystyle\cos\frac{A'}{2}+\cos\frac{B'}{2}+\cos\frac{C'}{2}}\le\frac{3\sqrt{3}R'}{a'+b'+c'}\right)$
- Points on Incircle: Another Look $\left(\displaystyle 5r\le\frac{PA^2}{h_a}+\frac{PB^2}{h_b}+\frac{PC^2}{h_c}\le\frac{5}{2}R\right)$
- An All-Inclusive Inequality $\left(\displaystyle\frac{m_am_bm_c}{r_ar_br_c}+\frac{\ell_a\ell_b\ell_c}{h_ah_bh_c}\leq \frac{R}{r}\right)$
- An All-Inclusive Inequality II $\left(\displaystyle\left(\sum_{cycl}\sqrt{\frac{m_a}{\ell_a}}\right)\left(\sum_{cycl}\sqrt{\frac{m_a}{h_a}}\right)\le\frac{9R}{2r}\right)$
- Inequality with Roots, Squares and the Area $(\displaystyle \sqrt{2}(PA+PB+PC)\ge\sqrt{a^2+b^2+c^2+4\sqrt{3}S})$
- A One-Sided Inequality in Triangle $\left(\displaystyle BA'\cdot CB'\cdot AC' + BA''\cdot CB''\cdot AC'' + BA'''\cdot CB'''\cdot AC''' \lt \frac{3abc}{8}\right)$
- Dan Sitaru's Inequality with Tangents $(\displaystyle\sum_{cycl}\sqrt[3]{\tan A}\sqrt[3]{\tan B}(\sqrt[3]{\tan A}+\sqrt[3]{\tan B})\le 2\tan A\tan B\tan C)$
- Dan Sitaru's Inequality with Tangents II $(\displaystyle \sum_{cycl}\tan A\tan B + 45^{\circ}\le 2\tan^2A\tan^2B\tan^2C)$
- Dan Sitaru's Inequality with Roots and Powers $(\displaystyle (\sqrt{a}+\sqrt{b}+\sqrt{c})^4(\sqrt[3]{a}+\sqrt[3]{b}+\sqrt[3]{c})^6\ge 2^43^9S^2)$
- A Cyclic Inequality in Triangle $\left(\displaystyle\sum_{cycl}\frac{a^3(2s-a)}{b(2s-b)}\ge\frac{27a^2b^2c^2}{s^2}\right)$
- A Cyclic Inequality in Triangle II $\left(\displaystyle\sqrt{abc}\left(\frac{a^2}{\sqrt{b}}+\frac{b^2}{\sqrt{c}}+\frac{c^2}{\sqrt{a}}\right)^2\ge 16(\sqrt{a}+\sqrt{b}+\sqrt{c})S^2\right)$
- Inequality with Cubes and Cube Roots $(\displaystyle\sum_{cycl}(\sqrt[3]{a}+\sqrt[3]{b}-\sqrt[3]{c})^3\ge\sqrt[3]{3a}+\sqrt[3]{3b}+\sqrt[3]{3c}-2)$
- Tangent, Cotangent and Square Roots Inequality $(\displaystyle\left(\sum_{cycl}\sqrt{\cot A\cot B}\right)\left(\sum_{cycl}\sqrt{\tan A\cot B}\right)\ge 3\sqrt{3})$
- An Inequality with Sines $\left(\displaystyle \prod_{cycl}\left(\frac{2}{\sin A}-1\right)\ge\left(\frac{6}{\sin A+\sin B+\sin C}-1\right)^3\right)$
- An Inequality in Triangle, with Sines II $\left(\displaystyle \left(\sum_{cycl}\frac{\sin A}{\sin B}\right)\left(\sum_{cycl}\frac{\sin A}{\sin^2 B}\right)\left(\sum_{cycl}\frac{\sin A}{\sin^3 B}\right)\ge 24\sqrt{3}\right)$ $\left(\displaystyle\sin^22A+\sin^22B+\sin^22C\le\sin^2A+\sin^2B+\sin^2C\right)$
- An Inequality with Tangents and Cotangents $\left(\displaystyle\prod_{cycl}\left(\tan\frac{A}{2}\tan\frac{B}{2}+\cot\frac{A}{2}\cot\frac{B}{2}\right)\ge\frac{1000}{27}\right)$
- An Inequality with Sides and Medians $(2am_a\le bm_c+cm_b)$
- An Inequality in Triangle with Sides and Medians II $\left(\displaystyle 16\sum \Bigr(\frac{m_a}{m_c}+\frac{m_b}{m_c}\Bigr)^4\gt 81\Biggl(\Bigr(\frac{a}{m_a}\Bigr)^4+\Bigr(\frac{b}{m_b}\Bigr)^4+\Bigr(\frac{c}{m_c}\Bigr)^4\Biggl)\right)$
- An Inequality with Sin, Cos, Tan, Cot, and Some $(2S^2\displaystyle\sum_{cycl}(\sin A+\cos A+\tan A+\cot A)\gt 81\pi R^4\prod_{cycl}\cos A)$
- Leo Giugiuc's Second Lemma And Applications $(3(a+b)\gt 2(m_a+m_b))$
- An Inequality with Arctangents in Triangle $\left(\displaystyle\frac{a^3\cos^3A}{\arctan\frac{1}{2}}+\frac{b^3\cos^3B}{\arctan\frac{1}{5}}+\frac{c^3\cos^3C}{\arctan\frac{1}{8}}\ge\frac{32r^3s^3}{3\pi R^3}\right)$
- An Inequality in Triangle with Roots and Circumradius $(\displaystyle a\sqrt{b}+b\sqrt{c}+c\sqrt{a}\le 3R\sqrt{2s})$
- An Inequality for the Cevians through Circumcenter $\left(\displaystyle \frac{A_1O}{OA}+\frac{B_1O}{OB}+\frac{C_1O}{OC}=\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{x+y}\ge\frac{3}{2}\right)$
- An Inequality with Powers of Six $(\displaystyle a^6+b^6+c^6\ge 8r^2s\sum_{cycl}\frac{a^5}{b^2-bc+c^2})$
- Adil Abdullayev's Inequality With Roots and Powers $\left(\displaystyle a^2+b^2+c^2\ge 4S\cdot\sqrt[4]{(a^2+b^2+c^2)\left(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\right)}\right)$
- Marian Cucoanes' Inequality With Roots and Powers $\left(\displaystyle \small{a^2+b^2+c^2\ge 4S\cdot\sqrt{\frac{1}{2}(a^2+b^2+c^2)\left(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\right)-\frac{3}{2}}}\right)$
- Marian Dinca's Inequality $\left(\displaystyle m_a\le\frac{s}{\sqrt{3}}\right)$
- An Inequality for the Cevians through Spieker Point via Brocard Angle $(a^2b^2+b^2c^2+c^2a^2 ≥ 2s(AC'\cdot BA'\cdot CB' + AB'\cdot BC'\cdot CA'))$
- Hung Nguyen Viet's Inequality with Radicals and Chebyshev $\left(\displaystyle\sum_{cycl}(a-\sqrt{bc})\sin\frac{A}{2}\ge 0\right)$
- An Inequality in Triangle, Mostly with the Medians $(\displaystyle \prod_{cycl}(5m_a+3m_b)(3m_a+5m_b)\lt 64\prod_{cycl}(2s+a)^2)$
- An Inequality in Triangle with Altitudes, Medians And Symmedians $\left(\displaystyle \frac{A_2A_3}{A_1A_2}\cdot\frac{B_2B_3}{B_1B_2}\cdot\frac{C_2C_3}{C_1C_2}\gt\prod_{cycl}\frac{(a+b-c)^2}{2a^2+2b^2-c^2}\right)$
- An Inequality with Altitudes and Medians $(\sqrt{3}\max (h_a,h_b,h_c)\ge s \ge \sqrt{3}\min (m_a,m_b,m_c))$
- An Inequality with Altitudes and Angle Bisectors $(\max (h_a,h_b,h_c)\ge \min (\ell_a,\ell_b,\ell_c))$
- Leo Giugiuc's Inequality for the Medians $(m_a+m_b+m_c\le\sqrt{3s^2+\frac{3}{4}[(a-b)^2+(b-c)^2+(c-a)^2]})$
- An Inequality in Triangle with Medians, Sides and Circumradius $(\displaystyle m_a\ge\frac{b^2+c^2}{4R})$
- An Inequality In Triangle with Sines of Half-Angles $\displaystyle\left( \sin\frac{A}{2}+\sin\frac{B}{2}+\sin\frac{C}{2}\le 2\sum_{cycl}\frac{a}{(\sqrt[3]{b}+\sqrt[3]{c})(\sqrt[3]{b^2}+\sqrt[3]{c^2})}\right)$
- An Inequality in Triangle with the Sines of Half-Angles and Cube Roots $\displaystyle\left( 2\sum_{cycl} \left(\frac{a}{b}+\frac{b}{a}\right)\sin^2 \frac{C}{2}\geq \sqrt[3]{abc}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\right)$
- An Inequality in Triangle with the Circumradius, Inradius and Angle Bisectors $(R+r\ge\min (\ell_a,\ell_b,\ell_c))$
- An Inequality in Triangle with Differences of the Medians $\displaystyle\left(\frac{8(m_a-m_b)(m_b-m_c)(m_c-m_a)}{(b-a)(c-b)(a-c)}>\frac{27abc}{(a+2s)(b+2s)(c+2s)}\right)$
- Problem 4087 from Crux Mathematicorum $( m_a(b+c)+2m_a^2\ge 4S\sin A)$
- An Inequality with Inradius and Circumradii $\left(\displaystyle (R_a+R_b+R_c)\left(\frac{R_a}{R_bR_c}+\frac{R_b}{R_cR_a}+\frac{R_c}{R_aR_b}\right)\ge 12-\frac{6r}{R}\right)$
- An Inequality in Triangle, with Integrals $\left(\displaystyle 4\sum_{cycl}\sin^2\frac{a}{2}+\pi\sum_{cycl}\int_{0}^{a}\cos (\sin x)dx\ge \pi^2\right)$
- An Inequality in Triangle, with Sines $\displaystyle\left(\prod_{cycl}\left(\frac{2}{\sin A}-1\right)\ge\left(\frac{6}{\sin A+\sin B+\sin C}-1\right)^3\right)$
- An Inequality in Triangle, with Sides and Sums $\left(\displaystyle \frac{a(2s-a)}{4(s-a)}+\frac{a(2s-b)}{4(s-b)}+\frac{a(2s-c)}{4(s-c)}\ge a+b+c\right)$
- An Inequality with a Variety of Circumradii $\left(\displaystyle \frac{R_a^2}{R_b}+\frac{R_b^2}{R_c}+\frac{R_c^2}{R_a}\geq 3R\right)$
- Dorin Marghidanu's Inequality with Maximum Side $\left(\displaystyle h_a \le \frac{p}{\sqrt{3}}\right)$
- An Inequality with Circumradii And Distances to the Vertices $\displaystyle\left(\frac{MB\cdot MC}{R_a}+\frac{MC\cdot MA}{R_b}+\frac{MA\cdot MB}{R_c}\le MA+MB+MC\right)$
- An inequality with Cosines and a Sine $\displaystyle\left(\cos A+4\cos B+4\sin\frac{C}{2}\le 9\cos\frac{\pi+B-C}{3}\right)$
- An inequality with Three Points $\displaystyle\left(\sum_{P\in\{O,I,G\}}\sum_{cycl}\left(\frac{[\Delta APB]}{[\Delta ABC]}+\frac{[\Delta ABC]}{[\Delta APB]}\right)^2\ge 100\right)$
- An Inequality with One Tangent and Six Sines $\left(\displaystyle \frac{\tan A}{\sin B+5\sin C}+\frac{\tan B}{\sin C+5\sin A}+\frac{\tan C}{\sin A+5\sin B}\gt\frac{1}{2}\right)$
- An Inequality with Tangents and Sides $\left(\displaystyle \frac{a^2}{\tan B+\tan C}+\frac{b^2}{\tan C+\tan A}+\frac{c^2}{\tan A+\tan B}\leq sR\right)$
- An Inequality with Sides, Altitudes, Angle Bisectors and Medians $\left(\displaystyle \left(\frac{h_b}{m_a}+\frac{h_c}{m_b}+\frac{h_a}{m_c}\right)\left(\frac{h_b}{\ell_a}+\frac{h_c}{\ell_b}+\frac{h_a}{\ell_c}\right)\ge\left(\frac{b}{a}+\frac{c}{b}+\frac{a}{c}\right)^2\right)$
- An Inequality of the Areas of Triangles Formed by Circumcenter And Orthocenter $\left(\displaystyle \sum_{cycl}\sqrt[n]{[\Delta OAB]}\ge\sum_{cycl}\sqrt[n]{[\Delta HAB]}\right)$
- An Inequality with Angle Trisectors $\left(\displaystyle \frac{AE}{AB}+\frac{AF}{AC}\lt 2\right)$
- An Inequality for Sides and Area $\left(\displaystyle \sum_{cycl}\frac{(a^2-ab+b^2)^2}{a^2+4ab+b^2}\ge\frac{2S}{\sqrt{3}}\right)$
- A Cyclic Inequality in Triangle for Integer Powers $\left(\displaystyle \sum_{cycl}\frac{a^{n+1}}{b+c-a}\ge\sum_{cycl}a^n\right)$
- R and r When G on Incircle $(8R\ge 25r)$
- An Inequality for Cevians And The Ratio of Circumradius and Inradius $\left(\displaystyle \frac{XB}{XY}\cdot\frac{YC}{YZ}\cdot\frac{ZA}{ZX}\le\frac{R}{2r}\right)$
- Centroid on the Incircle in Right Triangle $\left(648Rr\ge 25 (a^2+b^2+c^2)\right)$
- An Inequality with Cotangents And the Circumradius $\left(\displaystyle \sum_{cycl}a^2\cot B\cot C\le 4R^2\right)$
- An Inequality with Inradius and Excenters $\left(\displaystyle \sum_{cycl}\frac{1}{II_a^2}+\sum_{cycl}\frac{1}{I_aI_b^2}\le\frac{1}{4r^2}\right)$
- An Inequality with Inradius and Side Lengths $\left(\displaystyle \sum_{cycl}(b+c-a)^2\cdot\sum_{cycl}(b+c-a)^3\ge 2592\sqrt{3}r^5\right)$
- An Inequality with Exradii and an Altitude $\left(\displaystyle \sqrt{\frac{1}{r_b^2}+\frac{1}{r_c}+1}+\sqrt{\frac{1}{r_c^2}+\frac{1}{r_b}+1}\ge 2\sqrt{\frac{1}{h_a^2}+\frac{1}{h_a}+1}\right)$
- Leuenberger's Inequality for Medians, Inradius and Circumradius $\left(\displaystyle m_a+m_b+m_c\le 4R+r\right)$
- Adil Abdulayev's Inequality With Angles, Medians, Inradius and Circumradius $\left(\displaystyle \frac{A}{m_a}+\frac{B}{m_b}+\frac{C}{m_c}\le \frac{3\pi}{4R+r}\right)$
- An Inequality with Sides, Cosines, and Semiperimeter $\left(\displaystyle \sum_{cycl}a^2(b\cos B+c\cos C)\le \frac{8s^3}{9}\right)$
- Seyran Ibrahimov's Inequality $\left(\displaystyle \sqrt{3}s\cdot\sum_{cycl}m_a\le 20R^2+r^2\right)$
- An Inequality in Triangle, with Sides and Medians III $\left(\displaystyle \sum_{cycl}\frac{(m_b+m_c-m_a)^3}{m_a}\ge\frac{3}{4}(a^2+b^2+c^2)\right)$
- Leo Giugiuc's Inequality in Triangle, Solely with Cotangents $\left(\cot A +\cot B+\cot C\ge 2\sqrt{2}-1\right)$
- An Inequality in Triangle with Side Lengths and Circumradius $\left(\displaystyle\displaystyle\frac{ab}{\sqrt{a^2+b^2}}+\frac{bc}{\sqrt{b^2+c^2}}+\frac{ca}{\sqrt{c^2+a^2}}\le\frac{3\sqrt{6}R}{2}\right)$
- All Trigonometric Inequality in Triangle $\left(\displaystyle 3\sum_{cycl}\cos A\ge 2\sum_{cycl}\sin A\sin B\right)$
- An Inequality with Two Sets of Cevians $\left(\displaystyle \frac{27[A'B'C']}{[A''B''C'']}\leq \Bigr(\frac{BA'}{BA''}+\frac{CB'}{CB''}+\frac{AC'}{AC''}\Bigr)^3\right)$
- An Inequality with the Most Important Cevians $\left(\displaystyle \frac{m_am_bm_c}{h_ah_bh_c}\ge\frac{\ell_a^2+\ell_b^2+\ell_c^2}{\ell_a\ell_b+\ell_b\ell_c+\ell_c\ell_a}\right)$
- An Inequality in Triangle with a Constraint $(a\sqrt{2}\ge b+c)$
- Problem 11984 From the American Mathematical Monthly $\left(\displaystyle a^6+b^6+c^6\ge 5184\cdot r^6\right)$
- A Long Cyclic Inequality of Degree 4 $\left(\displaystyle 4\cdot\sum_{cycl}ab\cdot\sum_{cycl}a-\left(\sum_{cycl}a\right)^3\ge\frac{\displaystyle 3\sum_{cycl}ab\left[4\sum_{cycl}ab-\left(\sum_{cycl}a\right)^2\right]}{\displaystyle \sum_{cycl}a}\right)$
- An Inequality of Degree 3 with Inradius $\left(\displaystyle \sum_{cycl}(a+b-c)^3+24abc\ge 648\sqrt{3}r^3\right)$
- A Cyclic Inequality from the 6th IMO, 1964 $\left(\displaystyle \sum_{cycl}a^2(b+c-a)\le 3abc\right)$
- An Area Inequality in Right Triangle $\left(\displaystyle \frac{[\Delta ABD]+[\Delta ACE]}{[\Delta ADE]}\ge\sqrt{2}\right)$
- An Angle Inequality in Triangle with Perpendicular Medians $\left(\displaystyle \cos A\ge \frac{4}{5}\right)$
- An Inequality in Triangle form the 1996 APMO $\left(\sqrt{a+b-c}+\sqrt{b+c-a}+\sqrt{c+a-b}\le\sqrt{a}+\sqrt{b}+\sqrt{c}\right)$
- An Inequality in a Nonobtuse Triangle $\left(R\sqrt{2}\le h_a\right)$
- An Inequality in Triangle with Radicals, Semiperimeter and Inradius $\left(\displaystyle \sqrt{\frac{a+b}{s-b}}+ \sqrt{\frac{b+c}{s-c}} +\sqrt{\frac{c+a}{s-a}}\le \frac{\sqrt{a^2+b^2+c^2}}{r}\right)$
- Dan Sitaru's Inequality with Radicals and Cosines $\left(\displaystyle (a^2+b^2+c^2)^3\ge 6^3(abc)^2\cos A\cos B\cos C\right)$
- Lorian Saceanu's Cyclic Inequalities with Three Variables $\left(\displaystyle 2+\sum_{cycl}\frac{a}{b}\ge \sum_{cycl}\frac{a}{c}+2\frac{ab+bc+ca}{a^2+b^2+c^2}\right)$
- An Inequality for the Tangent to the Incircle $\left(\displaystyle DE\le\frac{1}{8}(AB+BC+CA)\right)$
- Lorian Saceanu's Sides And Angles Inequality $\left(\displaystyle \frac{\pi}{3}\le \frac{a\alpha + b\beta + c\gamma}{a+b+c}\le \arccos\left(\frac{r}{R}\right)\right)$
- An Inequality in Triangle with Radicals, Semiperimeter, Incenter and Inradius $\left(\displaystyle \frac{AI+BI+CI}{r}+3\ge\left(\sum_{cycl}\sqrt{s-a}\right)\left(\sum_{cycl}\frac{1}{\sqrt{s-a}}\right)\right)$
- An Inequality in Triangle for Side Lengths, Cycled in Two Ways $\left(\displaystyle 3\left(\frac{a}{b}+\frac{b}{c}+\frac{c}{a}-1\right)\ge 2\left(\frac{b}{a}+\frac{a}{c}+\frac{c}{b}\right)\right)$
- Lorian Saceanu's Inequality for All Triangles $\left(\displaystyle \sin 2A+\sin 2B+\sin 2C\ge 4\sin 2A\cdot\sin 2B\cdot\sin 2C\right)$
|Contact| |Up| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73578886
