Padoa's Inequality

Let in $\Delta ABC,\,$ $a=y+z,\,$ $b=z+x,\,$ $ c=x+y.$

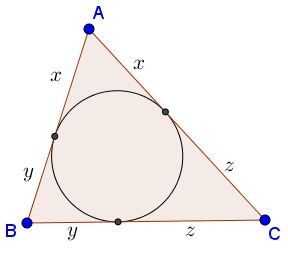
Padoa's inequality, illustration

Then

$abc\ge 8xyz.$

Indeed, by the AM-GM inequality,

$abc=(y+z)(z+x)(x+y)\ge 2\sqrt{yz}\cdot 2\sqrt{zx}\cdot 2\sqrt{xy}=8xyz.$

Now $x,y,z\,$ can be expressed in terms of $a,b,c:$

$\displaystyle\begin{align} x &= \frac{b+c-a}{2},\\ y &= \frac{a+c-b}{2},\\ z &= \frac{a+b-c}{2}. \end{align}$

which rewrites the above inequality into

known as Padoa's inequality after Alessandro Padoa (1868-1937). Dorin Marghidanu came up with an interesting refinement of the inequality.

Leo Giugiuc observes that a more general statement is also true:

If $a,b,c\gt 0$ then

$(b+c-a)(c+a-b)(a+b-c)\le abc.$

For a proof, let, WLOG, $a=\max\{a,b,c\}.$ If $b+c-a\le 0,$ hen $c+a-b\gt 0$ and $a+b-c\gt 0,$ implying

$(b+c-a)(c+a-b)(a+b-c)\le 0\lt abc.$

If $b+c-a\gt 0,$ then also $c+a-b\gt 0$ and $a+b-c\gt 0,$ meaning that $a,b,c$ form a triangle and reducing the problem to the case already discussed.

71546526