From Leningrad Mathematical Olympiad

Urquhart's Theorem - 2 Solutions From Leningrad Mathematical Olympiad

Urquhart's Theorem was a subject of problem 61 at the 55^th Leningrad Mathematical Olympiad (1989) for grade 9. The problem, with two solutions, appeared in a collection that has been published by MathPro press. Below, I shall preserve the notations from the book, which are different from those used elsewhere at the site.

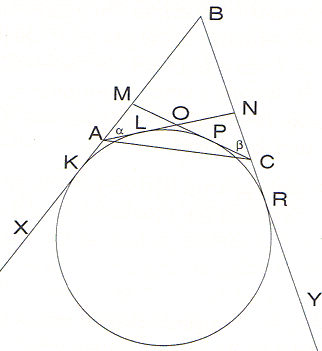
With a reference to the figure below, points M and N are chosen on the sides AB and BC of triangle ABC, respectively, so that AM + AN = CM + CN. Segments CM and AN intersect at point O. Prove that AO + AB = CO + CB.

Solution 1

Denote angles MAO and NCO by letters α and β, respectively. Squaring the equality AM + AN = CM + CN gives AM² + AN² + 2AM×AN = CM² + CN² + 2CM×CN. Further, applying the law of cosines to triangles AMN and CMN, we have

AM² + AN² - 2AM×AN cos α = CM² + CN² - 2CM×CN cos β

(both sides of this equality are equal to MN²). So, we can obtain the important relation

AM×AN(1 + cos α) = CM×CN(1 + cos β),

which will be used later. We begin by focusing on segments AO, AB, CO, CR. The law of cosines for triangles AOB and BOC gives

AO² + AB² - 2AO×AB cos α = CO² + CR² - 2CO×CB cos β.

So, to obtain the desired equality AO + AB = CO + CB, we have to show that the relation

AO×AB(1 + cos α) = CO×CB(1 + cos β)

holds true. Thus, we must prove the equality

AO×AB

AM×AN

CO×CB

CM×CN

which will complete the solution. Let's write the law of sines for triangles AMO, NOC, ANB, BMC:

	AO / AM	= sin(∠AMO) / sin(∠AOM),
	CO / CN	= sin(∠ONC) / sin(∠NOC),
	BC / MC	= sin(∠BMC) / sin(∠MBC),
	AN / AR	= sin(∠MBC) / sin(∠BNA).

Since sin(180° - x) = sin x, we see that sin(∠BNA) = sin(∠ONC) and sin(∠BMC) = sin(∠AMO); also, sin(∠AOM) = sin(∠NOC). Hence, the relations written above imply the promised equality.

Solution 2

The key fact of the second solution is that both equalities AM + AN = CM + CN and AO + AR = CO + CR are equivalent to the assertion that one can inscribe a circle in "quadrilateral" XAOCY (see the diagram). (We use quotation marks because the quadrilateral is infinite, and points X and Y here are not its vertices - they are two arbitrary points chosen on corresponding rays.) To avoid too many repetitions of lengthy notation, we introduce the following: Two points M, N chosen on sides AB, BC respectively, are called a right pair if it is possible to inscribe a circle in quadrilateral XAOCY formed by this choice of M and N. We show first that equality AM + AN = CM + CN implies that points M, N form a right pair, deducing this as a consequence of the following facts:

Fixed point N from segment BC determines the unique point M lying on segment AB such that pair M, N is right. It follows by observation that there exists a single circle inscribed in "triangle" XANY - its center is the intersection point of the bisectors of angles XAN and ANY.
Fixed point N from segment BC determines no more than one point M from segment AB that satisfies the equality AM + AN = CM + CN.

Proof

Assuming there exist two such points M₁ and M₂, we have AM₁ + AN = CM₁ + CN and AM₂ + AN = CM₂ + CN. Then subtraction of the first equality from the second brings us to

CM₂ - CM₁ = AM₂ - AM₁ = M₂M₁.

But the triangle inequality applied to triangle CM₂M₁ gives CM₂ - CM₁ < M₂M₁.

If points M, N lying on segments AB, BC, respectively, constitute a right pair, then AM + AN = CM + CN.

Proof

Denote the points at which the inscribed circle touches the sides of the equilateral corresponding to this choice of M, N by the letters K, L, P, R. Then we have the equalities AK = KL, LO = OP, PC = CR, MK = KP, NL = NR. Thus,

	AM + AN	= MK - AK + AL + LN
		= MK + LN
		= MP + NR
		= MP + PC - CR + NR
		= CM + CN.

Now, these three statements imply that if equality AM + AN = CM + CN holds true for some points M, N lying on segments AB, BC, then M, N form a right pair because otherwise one could find some point M' different from M forming a right pair with N, and we would have the equality AM' + AN = CM' + CN, which contradicts the second fact above.

Thus, to complete the solution we have to prove that if points M, N form a right pair, then the equality AO + AB = CO + CB is satisfied. The proof is very similar to that of the third fact above, and we leave it to the reader.

Note: Perhaps the second solution seems long, but this is caused by our attempt to supply an essentially geometric consideration. We'd like to stress the undoubted beauty of the idea of proving an equivalence of two given assertions using a third (not obvious) one, which is equivalent to each of them.

Reference

D. Fomin, A. Kirichenko, Leningrad Mathematical Olympiads 1987-1991, MathPro Press, 1994

Urquhart's Theorem

72088865