Proof by M. Cabart

Urquhart's Theorem For And By Conics

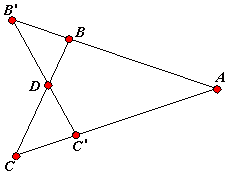
Urquhart's theorem states that, for straight lines ABB' and AC'C with BC and B'C' intersecting in D the relation AB + BD = AC' + C'D implies AB' + B'D = AC + CD, as when four lines displayed all touch the same circle.

Michel Cabart wondered whether an "hyperbolic" version of the theorem is also true:

Is BD - BA = C'D - C'A equivalent to B'D - B'A = CD - CA?

What follows is the combination of Michel's emails of December 9 and 15, 2008.

Using a trigonometric approach in analogy to the "circular theorem":

	(BD - BA) / AD	= (sin2β' - sin2β) / sin2(β + β')
		= [sin(β' - β) cos(β' + β] / sin(β' + β) cos(β' + β)
		= sin(β' - β) / sin(β' + β)
		= [sinβ' cosβ - sinβ cosβ'] / [sinβ' cosβ + sinβ cosβ']
		= (t - 1) / (t + 1)

by posing t = tanβ' / tanβ. Thus BD - BA = C'D - C'A iff tanβ' / tanβ = tanγ / tanγ' and the rest of the proof is similar.

The two variants of the theorem can be summarized into one single property: "If B and C' belong to an ellipse (resp. hyperbola), then B' and C also belong an ellipse (resp. hyperbola) with the same foci."

This suggests a proof by conics theorems. The following one (detailed for ellipse and similar for hyperbola) uses the following property of the focuses: for any two tangents MA and CA intersecting in A, FA bisects MFC and F'A bisects MF'C. Here we take CA perpendicular to the major axis.

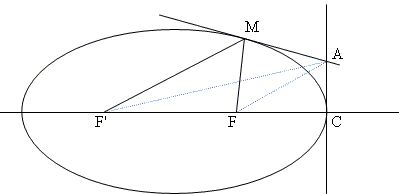
michel cabart's treatment of urquhart's theorem

Notations:

∠ MF'C = 2α' and ∠MFC = 2α,
c = half the distance between foci, a = half the length of the major axis.

We then have:

tanα' = AC / (a + c) and
tanα = AC / (a - c)

so that

tanα' / tanα = (a - c) / (a + c)

Thus returning to the problem: BD + BA = C'D + C'A iff

	tanβ' / tan(π/2 - β)	= (a - c) / (a + c)
		= tanγ / tan(π/2 - γ').

which is the condition found by trigonometric calculations.

Urquhart's Theorem

71931937