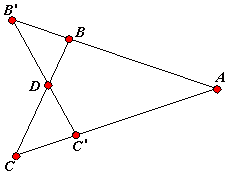
Urquhart's Theorem

If ABB' and AC'C are straight lines with BC and B'C' intersecting in D and if AB + BD = AC' + C'D, then AB' + B'D = AC + CD.

According to Dan Pedoe, the Australian mathematician M. L. Urquhart (1902-1966) discovered the theorem while working on "some fundamental concepts of the theory of special relativity." He dubbed it the most elementary theorem of Euclidean geometry since it only involves the concepts of straight line and distance. The theorem elicited some interest, especially, among problem solvers with several solutions appearing in Crux Mathematicorum in 1976. Unfortunately, I have no access to these discussions. On the other hand, Dan Pedoe came up with another curious result while pondering over the theorem. Pedoe also pointed to a book by I. M. Yaglom, where a relevant (and a more general) result have been proved in the context of directed lines, circles and distances. Pertinent definitions have been given by Darij Grinberg in an online discussion and by Stuart Anderson in a less formal framework. The notion of directed (signed) lines and distances allows one to consider a circle touching four lines without specifying the nature of tangency, whether in some sense the tangency is internal or external to one of the quadrilaterals formed by the four lines. However, looking at a couple of such quadrilaterals simultaneously does highlight the nature of the theorem.

The theorem and its proof have been included in the Which Way Did the Bicycle Go? collection with a short trigonometric proof and another such proof can be accessed online. A really short trigonometric proof has been recently published in Forum Geometricorum by M. Hajja. M. Hajja also found that De Morgan has published a proof of the theorem in 1841, and that the theorem is a limiting case of one by Chasles published in 1860. In a 1934 Russian article, the author remarks that the theorem has been treated by Pitot in 1725 and that Steiner improved on Pitot's result in 1846. It is also mentioned that M. Darboux gave a very simple proof based on the properties of tangents to conic sections.

Below, I present M. Hajja's proof.

First, we establish a

Lemma

Let in ΔABC, angles at A, B, C measure 2α, 2β, and 2γ, respectively. Let p(ABC) be the perimeter of the triangle. Then

Proof

We repeatedly use the Law of Sines and the addition formulae.

Now let's return to Urquhart's theorem. Denote the angles as shown in the diagram.

Observe that in triangles AB'D and ACD side AD is common, so that, applying the Lemma to each of the triangles, we see that they have equal perimeters iff tanβ' tan(90^o - γ') = tanγ tan(90^o - β):

p(AB'D) = p(ACD) iff tanβ' tan(90o - γ') = tanγ tan(90o - β)   iff tanβ' cotγ' = tanγ cotβ   iff tanβ' tanβ = tanγ tanγ'   iff p(ABD) = p(AC'D),

as desired.

(An elementary synthetic solution appears elsewhere.)

References

1. M. Hajja, A Very Short and Simple Proof of "The Most Elementary Theorem" of Euclidean Geometry, Forum Geometricorum, v 6 (2006), 167-169.
2. P. Karonne, On Escribed Quadrilaterals, Mathematical Education, v1., 1934, pp. 20-23 (in Russian)
3. J. Konhauser, D. Velleman, S. Wagon, Which Way Did the Bicycle Go?, MAA, 1996
4. D. Pedoe, The Most "Elementary" Theorem Of Euclidean Geometry, Math Magazine, vol 49, no 1 (Jan., 1976), 40-42