Urquhart's Theorem - An Elementary Synthetic Solution

An elementary synthetic proof of Urquhart's Theorem has been posted at Professor's Wu online forum at Berkeley. I am grateful to Professor W. McWorter for pointing me in the right direction. Hereby I acknowledge lifting their solution along with the notations that happen to be different from those I used elsewhere.

With a reference to the figure below, if AD + DF = AB + BF, then AE + EF = AC + CF.

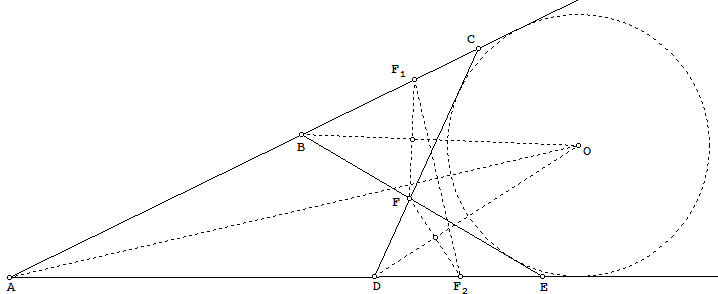
If we can show that, under given conditions, there exists a circle touching four lines AC, AD, CD, BE (prolonged, if needed – see the drawing), that the statement of the problem will follow.

To show that such a circle indeed exists, consider the ex-circles of triangles ACD and ABE (the ex-circle of a triangle is a circle tangent to 2 of its sides internally and one externally).

The center O₁ of the ex-circle of ACD is the intersection of angle bisectors A and CDE.

The center O₂ of the ex-circle of ABE is the intersection of angle bisectors A and CBE.

Now, consider the triangle FF₁F₂, where F₁, F₂ are chosen on corresponding lines such that BF₁ = BF, DF₂ = DF. Since

we get that all three triangles F₁AF₂, F₁BF, F₂DF are isosceles.

Therefore, the bisectors of angles A, CBE, CDE coincide with the bisectors of corresponding segments F₁F₂, FF₁, FF₂. But the latter 3 bisectors are concurrent, since they define the center of the circumcircle of the triangle F₁FF₂. Thus, O₁ and O₂ coincide.

Finally, the ex-circles of triangles ACD and ABE also coincide, since they touch the same two lines and are centered at the same point. But now it follows that this circle touches all four needed lines!

Urquhart's Theorem

• Urquhart's Theorem
• Proof by M. Cabart
• An elementary synthetic solution
• From Leningrad Mathematical Olympiad
• Pedoe's theorem
• Pitot theorem

|Contact| |Front page| |Contents| |Geometry| |Store|