Symmetries in Triangle II
What is this about?
Problem
Given point $P$ in the plane of $\Delta ABC,$ consider its reflections $X,$ $Y,$ $Z$ in the midpoints of sides $BC,$ $AC,$ and $AB,$ respectively.
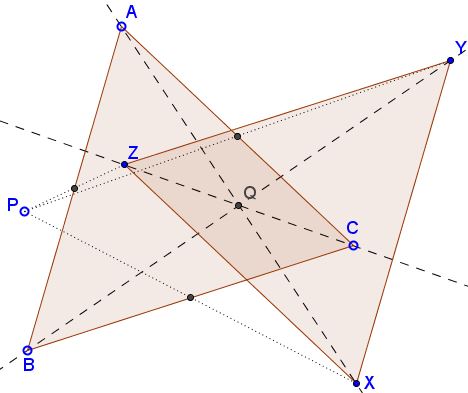
Then
- Lines $AX,$ $BY,$ $CZ$ are concurrent.
- Triangles $ABC$ and $XYZ$ are congruent.
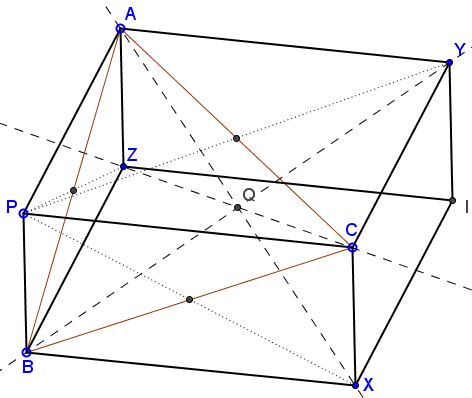
A 3D view
This page is an extension of an earlier one where the argument suggested by the diagram below has been discussed at length.
Synthetic solution
This is a solution by Emmanuel Antonio Jose García from his article A Note on Reflections.
Let $M_a,$ $M_b,$ $M_c$ be the midpoints of the sides $BC,$ $AC,$ $AB,$ respectively. Let $G$ be the centroid of $\Delta ABC.$
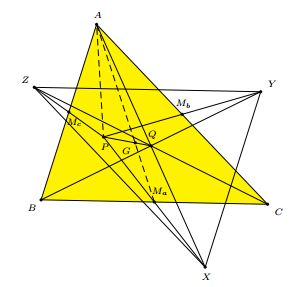
Consider $\Delta APX.$ It has the segment $AM_a$ as a median, and, its centroid $G$ $AM_a.$ If $Q$ is the midpoint of $AX,$ then $PQ$ is another median of $\Delta APX.$ Therefore, $G$ divides $PQ$ in the ratio $PG : GQ =2:1,$ and $Q$ is the complement of $P$.
Similarly, the same point $Q$ is the midpoint of $BY$ and $CZ.$ It follows that $\Delta XYZ$ is oppositely congruent to $\Delta ABC$ at $Q.$
Affine solution
The midpoint of side $BC$ is defined by $\displaystyle\frac{B+C}{2},$ whereas the fact that $X$ is the reflection of $A$ in that point tells us that it is also the midpoint of the segment $PX$ so that $\displaystyle\frac{B+C}{2}=\frac{P+X}{2},$ or,
$B+C=P+X.$
Similarly, $C+A=P+Y$ and $A+B=P+Z.$ Taking the difference of the latter two results in
$C-B=Y-Z,$
meaning that $BC=YZ$ and $BC\parallel YZ,$ or, in other words, that $BCYZ$ is a parallelogram whose diagonals $BY$ and $CZ$ intersect in their midpoints. Similarly we obtain that $AX$ and $BZ$ also share the midpoints, so that all three coincide. Finally, $BC=YZ$ and, similarly, $AB=XY$ and $AC=XZ,$ making triangles $ABC$ and $XYZ$ congruent.
Acknowledgment
I am grateful to Emmanuel Antonio Jose García for bringing his article to my attention.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73570258
