Moment of Inertia of a Regular Polygon
Problem
Let $A_{1}A_{2}\ldots A_{n-1}A_{n}$ be a regular polygon, $n\ge 3,$ with the circumcircle of radius $R.$ Let point $P$ lie on the circumcircle.
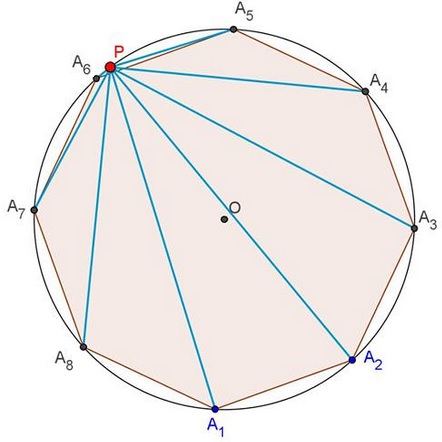
Prove that
$PA_{1}^{2}+PA_{2}^{2}+\ldots +PA_{n-1}^{2}+PA_{n}^{2}=2nR^{2}.$
Note that a dilation (homothety transformation) allows us to reduce the problem to the case of $R=1:$
Let $A_{1}A_{2}\ldots A_{n-1}A_{n}$ be a regular polygon, $n\ge 3,$ inscribed in the unit circle. Assume $P$ is also a point on the unit circle. Prove that
$PA_{1}^{2}+PA_{2}^{2}+\ldots +PA_{n-1}^{2}+PA_{n}^{2}=2n.$
Solution 1
Using complex numbers, place the center of the unit circle at the origin and the vertices at $A_{k}=e^{2(k-1)\pi i/n},$ $k=1,2, \ldots, n.$ Let $P=e^{\alpha i}.$ The task is to determine the sum, say,
$\begin{align}\displaystyle S_{n,P}&=\sum^{n-1}_{k=0}|e^{2(k-1)\pi i/n}-e^{\alpha i}|^{2}\\ &=\sum^{n-1}_{k=0}(e^{2(k-1)\pi i/n}-e^{\alpha i})(e^{-2(k-1)\pi i/n}-e^{-\alpha i})\\ &=2n-e^{-\alpha i}\sum^{n-1}_{k=0}e^{2(k-1)\pi i/n}-e^{\alpha i}\sum^{n-1}_{k=0}e^{-2(k-1)\pi i/n}. \end{align}$
$\displaystyle \sum^{n-1}_{k=0}e^{2(k-1)\pi i/n}=\frac{e^{2n\pi i/n}-1}{e^{2\pi i/n}-1}=0. $
And, similarly, $\displaystyle\sum^{n-1}_{k=0}e^{-2(k-1)\pi i/n}=\frac{e^{-2n\pi i/n}-1}{e^{-2\pi i/n}-1}=0.$
Solution 2
The problem is a particular case of a well-known theorem of Lagrange:
The moment of inertia of a system of material points relative to an arbitrary point $P$ is the sum of two quantities: the moment of inertia of the system relative to its center of gravity and the moment of inertia of the total mass placed at the center of gravity relative to $P.$
The theorem will be explained and treated elsewhere. Below, the focus is on the particular case at hand. Let's again assume $R=1$ and also $A_{k}=(x_{k},y_{k}),$ $k=1,2,\ldots,n,$ $P=(x,y).$ Finally, define the center of gravity $C=(x_{c},y_{c })$ with
$ \displaystyle x_{c}=\frac{1}{n}\sum_{k=1}^{n}x_{k},\\ \displaystyle y_{c}=\frac{1}{n}\sum_{k=1}^{n}y_{k}. $
These can also be written as $\displaystyle\sum_{k=1}^{n}(x_{k}-x_{c})=0$ and $\displaystyle\sum_{k=1}^{n}(y_{k}-y_{c})=0.$
For a regular polygon, the center of gravity coincides with its "geometric" center. In particular, $(x_{k}-x_{c})^{2}+(y_{k}-y_{c})^{2}=1,$ for every $k=1,2,\ldots n.$ The sum in question is
$\begin{align}\displaystyle S_{n,P}&=\sum^{n}_{k=1}\big[(x_{k}-x)^{2}+(y_{k}-y)^{2}\big]\\ &=\sum^{n}_{k=1}\big[x_{k}^{2}-2xx_{k}+x^{2}+y_{k}^{2}-2yy_{k}+y^{2}\big]\\ &=\sum^{n}_{k=1}(x_{k}^{2}+y_{k}^{2})-2x\sum^{n}_{k=1}x_{k}-2y\sum^{n}_{k=1}y_{k}+nx^{2}+ny^{2}\\ &=\sum^{n}_{k=1}(x_{k}^{2}+y_{k}^{2})-2nxx_{c}-2nyy_{c}+nx^{2}+ny^{2}\\ &=\sum^{n}_{k=1}(x_{k}^{2}+y_{k}^{2}-x_{c}^{2}-y_{c}^{2})+n\big[(x_{c}^{2}-2xx_{c}+x^{2})+(y_{c}^{2}-2yy_{c}+y^{2})\big]\\ &=\sum^{n}_{k=1}(x_{k}^{2}+y_{k}^{2}-x_{c}^{2}-y_{c}^{2})+n\big[(x_{c}-x)^{2}+(y_{c}-y)^{2}\big]\\ \end{align}$
Note now that, from the choice of $P,$ $(x_{c}-x)^{2}+(y_{c}-y)^{2}=1$ so that we may continue
$\begin{align}\displaystyle S_{n,P}&=\sum^{n}_{k=1}(x_{k}^{2}+y_{k}^{2}-x_{c}^{2}-y_{c}^{2})+n\big[(x_{c}-x)^{2}+(y_{c}-y)^{2}\big]\\ &=\sum^{n}_{k=1}(x_{k}^{2}+y_{k}^{2}-x_{c}^{2}-y_{c}^{2})+n\\ &=\sum^{n}_{k=1}\big[(x_{k}^{2}-2x_{k}x_{c}+x_{c}^{2})+(y_{k}^{2}-2y_{k}y_{c}+y_{c}^{2})\big]\\ &\,\,\,\,\,\,\,\,+2x_{c}\sum^{n}_{k=1}(x_{k}-x_{c})+2y_{c}\sum^{n}_{k=1}(y_{k}-y_{c})+n\\ &=\sum^{n}_{k=1}\big[(x_{k}-x_{c})^{2}+(y_{k}-y_{c})^{2}\big]+n\\ &=n+n=2n. \end{align}$
Acknowledgment
The problem has been posted by Dao Thanh Oai (Vietnam) at the CutTheKnotMath facebook page, Solution 2 is by Daniel Hardisky.
A modification of this problem appears elsewhere.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73608596
