Jordan Curve Theorem, Proof
- JCT - Topology Toolbox
- JCT - Prologue
- JCT - Simple Cases
- JCT - Abstract Graphs and Euler’s Formula
- JCT - K3,3 and the Crossed Arcs Lemma
- JCT - Jordan Separation - the general case
- JCT - Boundaries of the components of the complement of a Jordan curve - I
- JCT - The Jordan Arc theorem
- JCT - Boundaries of the components of the complement of a Jordan curve II
- JCT - Uniqueness of the bounded component of the complement
- JCT - K3,3 on a Torus or Moebius Strip
- JCT - Sources
JCT - K3,3 on a Torus or Möbius Strip
Scott E. Brodie, MD, PhD
Icahn School of Medicine at Mount Sinai
New York
$K_{3,3}\;$ is the "abstract graph" which connects each point in a set of three points to each point in another set of three points. We have shown that if the connections between points are drawn as continuous arcs, with no intersections except at their endpoints, such a graph cannot be realized on the plane (or on the sphere). However, if we allow ourselves to "think outside the plane," it is indeed possible to draw a realization of $K_{3,3},\;$ by working on slightly more complex surfaces, such as the torus or the Möbius strip.
$K_{3,3}\;$ on the torus
Begin by arranging the six points at the corners of a regular hexagon in the plane. If we number the points from $1\;$ to $6,\;$ our task is to connect all the odd-numbered points to all the even-numbered points, without allowing the connecting arcs to intersect other than at their endpoints.

The edges of the hexagon do most of the work, connecting point $1\;$ to points $2\;$ and $6;\;$ point $2\;$ to points $1\;$ and $3,\;$ and so on. Point $1\;$ can then be connected to point $\;4$ by an arc which runs in the exterior of the hexagon. Similarly, point $2\;$ can be connected to point $5\;$ by an arc which runs through the interior of the hexagon. But now we are stuck – there is no place in the plane to draw an arc from point $3\;$ to point $6,\;$ since the arcs $1-4\;$ and $2-5\;$ separate points $3\;$ and $6\;$ in both the interior and exterior of the hexagon.
Evidently, what is needed is a route bridging the separation of the two regions of (say) the interior of the hexagon by the arc $2-5.\;$ This can be supplied by attaching a "handle" to the plane, as shown in the figure. One can then, for example, attach this entire figure to a sphere with a suitable hole to obtain a surface which can easily be deformed into a standard torus, with $K_{3,3}\;$ inscribed.
A few more ways of visualizing $K_{3,3}\;$ on a torus are shown below. In the first, the torus is mapped to a "wallpaper pattern" which repeats endlessly on the plane, with opposite sides of the fundamental rectangular region to be mapped to each other ("identified") with orientations preserved (the top of the rectangle going left-to-right is identified with the bottom, also going left-to-right, and similarly the left side is identified bottom-to-top with the right side, bottom-to-top). This turns the fundamental rectangle into a surface resembling an "inner tube" of an automobile tire, i.e., a torus. The diagram shows how $K_{3,3}\;$ fits on the surface:
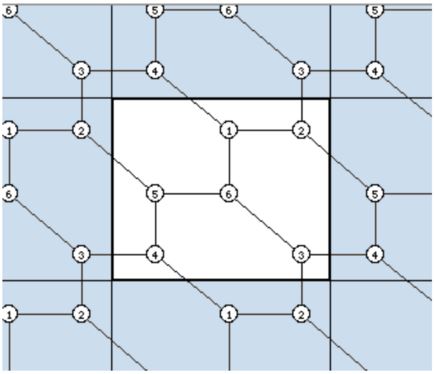
This is drawn on a three-dimensional depiction of he torus below left:
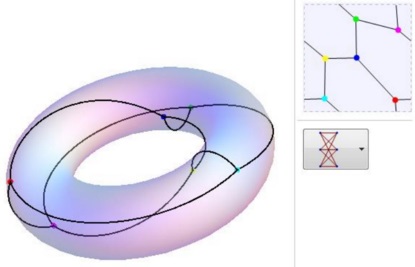
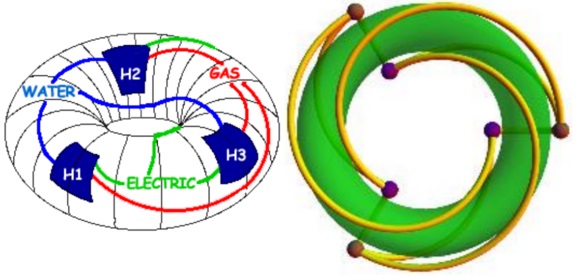
The figure below left shows how $K_{3,3}\;$ can be drawn on the torus and interpreted as the solution to the "Three Utilities Problem." A more symmetrical rendering of $K_{3,3},\;$ on the torus is shown below right
$K_{3,3},\;$ on the Möbius Strip
A Mobius strip is formed by taking a suitably long strip of paper and attaching (identifying) the ends, with a single "half-twist." This is shown in the figure below by means of the arrows on the right and left hand sides – the diagram is to be given a half-twist so that the arrows point in the same direction as the ends are joined. Evidently, as shown by the letters a and b, an arc in the outside of the hexagon from points $1\;$ to $4\;$ no longer separates points $3\;$ and $6,\;$ so $K_{3,3}\;$ can be drawn on the figure as shown:

A similar example is shown below, where the angular and circular shapes are to be matched up after the figure is given a half-twist, allowing the blue arcs to connect a blue and black dot, completing $K_{3,3}:\;$
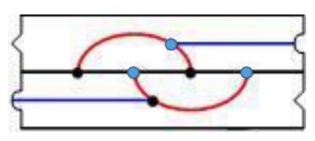
A $3$-dimensional visualization of $K_{3,3}\;$ on the Mobius strip is shown below:
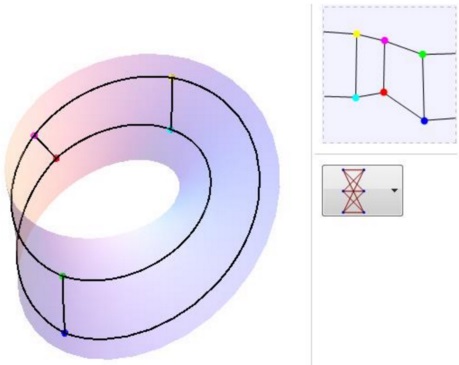
$K_{3,3}\;$ and the Jordan Curve Theorem
Elsewhere on these pages, the fact that $K_{3,3}\;$ cannot be realized in the plane was used to prove the Jordan Curve Theorem [that a continuous image in the plane of a circle separates the plane into two regions, an "inside" (a bounded region) and an "outside" (an unbounded region)]. It was demonstrated that the Jordan Curve Theorem does not hold on the torus or on the Möbius strip. The examples given here thus help illustrate how our proof of the Jordan Curve Theorem for the plane breaks down on the torus or the Möbius strip.
Jordan Curve Theorem, Proof
- JCT - Topology Toolbox
- JCT - Prologue
- JCT - Simple Cases
- JCT - Abstract Graphs and Euler’s Formula
- JCT - K3,3 and the Crossed Arcs Lemma
- JCT - Jordan Separation - the general case
- JCT - Boundaries of the components of the complement of a Jordan curve - I
- JCT - The Jordan Arc theorem
- JCT - Boundaries of the components of the complement of a Jordan curve II
- JCT - Uniqueness of the bounded component of the complement
- JCT - K3,3 on a Torus or Moebius Strip
- JCT - Sources
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73576300
