Jordan Curve Theorem, Proof
- JCT - Topology Toolbox
- JCT - Prologue
- JCT - Simple Cases
- JCT - Abstract Graphs and Euler’s Formula
- JCT - K3,3 and the Crossed Arcs Lemma
- JCT - Jordan Separation - the general case
- JCT - Boundaries of the components of the complement of a Jordan curve - I
- JCT - The Jordan Arc theorem
- JCT - Boundaries of the components of the complement of a Jordan curve II
- JCT - Uniqueness of the bounded component of the complement
- JCT - K3,3 on a Torus or Moebius Strip
- JCT - Sources
JCT - K3,3 and the Crossed Arcs Lemma
Scott E. Brodie, MD, PhD
Icahn School of Medicine at Mount Sinai
New York
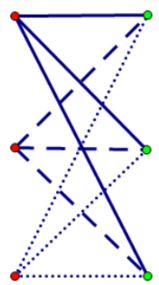
$K_{3,3}\;$ is the abstract graph obtained by from a set of $6$ points as follows: divide the points into two groups of three points, and connect each point in the first group to all three points in the second group.
The figure at right is not a realization of $K_{3,3},\;$ as many of the edges intersect at locations other than the $6$ vertices.
Indeed, we next use Euler’s formula to demonstrate that $K_{3,3}\;$ cannot be realized in the plane.
K3,3 is not planar
If $K_{3,3}\;$ can be realized in the plane with edges drawn as single line segments, Euler’s formula applies (as there are $6$ vertices and $9$ edges)
$F – 9 + 6 = 2.$
So $F = 5,\;$ that is, there must be $5$ faces.
But the defining structure of $K_{3,3}\;$ requires that each face must have an even number of edges; and as we do not allow edges to connect the same pair of vertices twice, each face must have at least $4$ edges. Counting up the edges by faces (as we did above), each edge is counted twice, so
$2E \ge 4F.$
And since $E = 9$ and $F = 5,$ we obtain $18 \ge 20.\;$ (!?!)
The contradiction proves that $K_{3,3}\;$ cannot be realized as a planar graph with edges composed of single line segments.
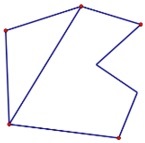
What if instead we are allowed to use polygonal arcs to try to realize $K_{3,3}\;$ In this case, let us distinguish the original vertices of the graph by calling them "nodes", and suppose that the maximal number of segments in the polygonal arcs connecting the nodes is $n.$ We can insert additional vertices in the arcs with fewer than $n$ segments and nudge the new vertices slightly to eliminate collinear adjacent segments. Then each arc will contain $n$ edges, and $n-1$ vertices, apart from the original nodes. As before, assuming this realization of $K_{3,3}\;$ is planar, we have
| 
|
|
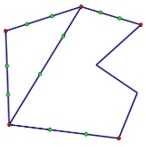
|
|
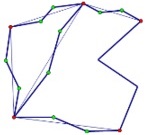
|
Lemma
If an abstract graph can be realized in the plane with Jordan arcs, then it can be realized in the plane with polygonal arcs as well.
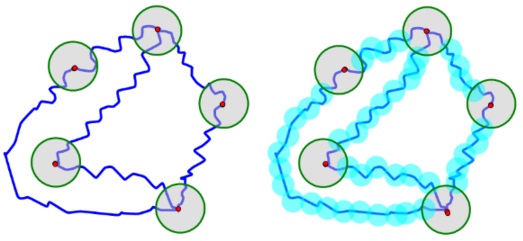
Proof
We may cover the nodes of the graph with small open discs, so that no two discs overlap.
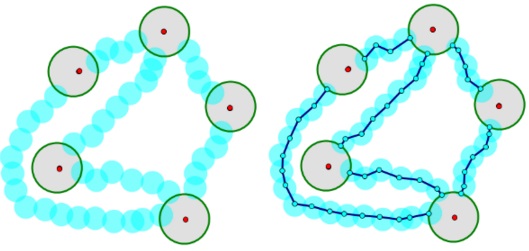
Now cover the disjoint Jordan arcs that remain between the discs with additional (overlapping) open discs, with radius less than half that of the smallest disc covering a node, such that these open covers are disjoint. (The discs covering the endpoints of the remaining Jordan arcs will of course overlap the discs which cover the original nodes.)
It is now easy to delete the original Jordan arcs, and replace them with polygonal arcs between the disks covering the nodes [Recall, any two points in a connected open set can be connected by a polygonal arc.] :
It is then a simple matter to add segments which connect the original nodes to the endpoints of the approximating polygonal arcs, so as to obtain a new set of polygonal arcs which reproduce the connections of the original graph, and the lemma is proved.
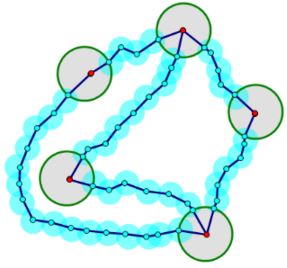
Now apply the Lemma to the question of whether $K_{3,3}\;$ can be realized in the plane using Jordan arcs to connect the vertices:
the answer is NO – if this could be done, $K_{3,3}\;$ could also be realized in the plane with polygonal arcs, contradicting Euler's formula.
[Here, we explicitly see why our proof does not extend to a torus or a Moebius strip.]
The Crossed Arcs Lemma
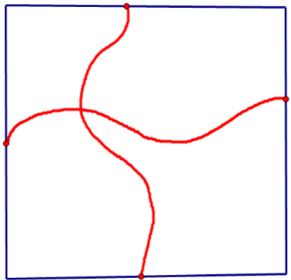
If one Jordan arc connects points of the upper and lower edges of a rectangle, and another connects points of the left and right edges of the rectangle, such that both arcs, except for their endpoints, fall in the interior of the rectangle, then the two arcs must intersect within the interior of the rectangle. (Both players cannot win the Game of Hex!)
Proof
Together with the upper left and lower right corners of the rectangle, the $4$ endpoints of the arcs can be colored, say, red and green in alternation going counterclockwise around the perimeter of the rectangle.
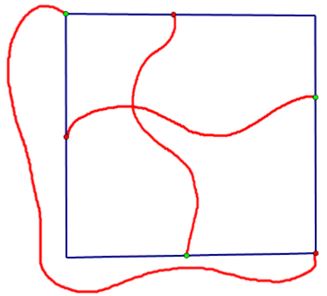
Connect the upper left and lower right corners with an arc in the exterior of the rectangle.
If the two original arcs do not intersect, this figure realizes $K_{3,3}\;$ with the colors indicating the two sets of three points. (Some of the connections are portions of the perimeter of the rectangle.) As this is impossible, the crossed arcs must intersect.
Jordan Curve Theorem, Proof
- JCT - Topology Toolbox
- JCT - Prologue
- JCT - Simple Cases
- JCT - Abstract Graphs and Euler’s Formula
- JCT - K3,3 and the Crossed Arcs Lemma
- JCT - Jordan Separation - the general case
- JCT - Boundaries of the components of the complement of a Jordan curve - I
- JCT - The Jordan Arc theorem
- JCT - Boundaries of the components of the complement of a Jordan curve II
- JCT - Uniqueness of the bounded component of the complement
- JCT - K3,3 on a Torus or Moebius Strip
- JCT - Sources
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73585925
