Jordan Curve Theorem, Proof

JCT - Uniqueness of the bounded component of the complement

Scott E. Brodie, MD, PhD
Icahn School of Medicine at Mount Sinai
New York

Suppose otherwise; then there are at least two disjoint bounded connected open regions in the complement of the Jordan curve, in addition to the unique unbounded component.
Partition the Jordan curve into three Jordan subarcs, which intersect only in their endpoints. Choose a point in the exterior of the curve; from this point, draw three disjoint arcs to accessible points within each of the three subarcs of the original curve.
Similarly, draw an arc within one of the interior components from an interior point to accessible points, one in each subarc, different from the accessible points used in the previous step.
Now draw an arc from an interior point of the other bounded component to 3 more different accessible points in each of the three subarcs.
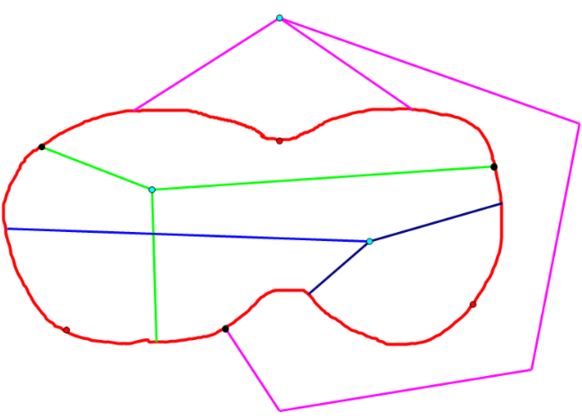
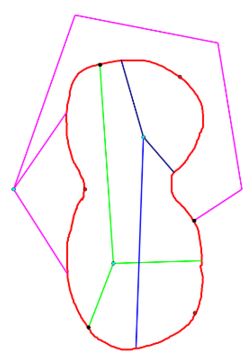
As previously, these three arcs cannot intersect any of the arcs previously drawn from the other two chosen points, as the three components of the complement are disjoint.
But if this is the case, we have drawn a realization of $K_{3,3}\;$ in the plane, which does not exist! [In the figure, the two sets of three points which are the nodes of $K_{3,3}\;$ are depicted in black and turquoise.]
The contradiction demonstrates that there are at most two (hence exactly two) components of the complement of the Jordan curve, Q.E.D.

71535057