Jordan Curve Theorem, Proof

JCT - Topology Toolbox

Scott E. Brodie, MD, PhD

We will work more or less interchangeably in the real line $\mathbb{R}$ and the ordinary Euclidean plane $\mathbb{E}=\mathbb{R}^2,$ and make no attempt at maximal generality.

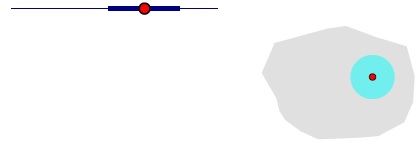
In $\mathbb{R}$, a set is open if every point in the set lies in an open interval in the set. In $\mathbb{E},$ a set is open if every point in the set lies in an open disc in the set:
A set is closed if its complement is open.

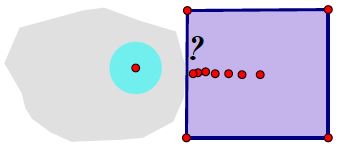
2.1. A closed set contains the limit of any convergent sequence of points in the set: If not, then such a sequence has a limit in the complement of the set, which is open. But the open set must contain a disc or interval surrounding the limit point, disjoint from the closed set. This contradicts the definition of limit:

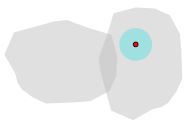
2.2. The complement of an open set is closed.
2.3. The union of open sets is open, as the intervals or discs in each of the original sets serve for the union as well.

2.4. It follows that the intersection of closed sets is closed.
2.5. These unions and intersections are arbitrary – the family of sets in the union or intersection can be finite, countably infinite, or even uncountably infinite.

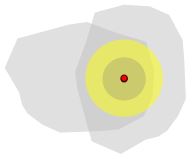
2.6. The intersection of two open sets is open, for we can use the minimum of the radii of the discs which surround a common point within each of the open sets to find a disc (or interval) which surrounds the common point and lies within both of the two sets:

2.7. By induction, the intersection of any finite collection of open sets is open.

2.8. But it is not true that an arbitrary intersection of open sets is open, or an arbitrary union of closed sets is closed – consider the intersection of an infinite nested set of open discs whose radius converges to $0,$ for example, or the union of the set of closed intervals of the form $\{[\frac{1}{n},\;1 {– \frac{1}{n}}]\}.$

2.9. And likewise the union of a finite collection of closed sets is closed.
A function $f$ is continuous at a point $x$ in its domain if for each interval (or disc) surrounding $f(x),$ there is an interval (or disc) surrounding $x$ in the domain which is mapped entirely into the interval (or disc) surrounding $f(x)$ in the range.

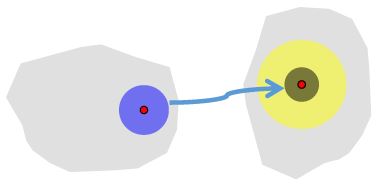
3.1. A function is continuous on a subset $S$ of its domain if it is continuous at every point in $S.$
The inverse image of a point $y$ in the range of a function $f$ is the subset of points in the domain which $f$ maps to $y.$ The inverse image of a subset of the range of a function is the subset of the domain which the function maps to the designated subset of the range.

4.1. A function is continuous whenever the inverse image of every open set in the range is open in the domain, since inverse images of functions preserve inclusions. (This is often paraphrased as "Inverse images take open sets backwards.")

4.2. Since open and closed sets are complementary, a function is likewise continuous whenever the inverse image of every closed set in the range is closed in the domain.
If a continuous function $f$ is one-to-one, its inverse relation is itself a function, which is often denoted $f^{-1}.$ If, in addition, the inverse function is itself continuous, the function is called a homeomorphism, and the domain and range are said to be homeomorphic, or each is said to be a homeomorphic image of the other.
5.1. Every continuous function takes open sets backwards; a homeomorphism takes open sets forwards as well, since the original function is the inverse of its inverse. Since continuity is defined as well by closed sets, a homeomorphism takes closed sets forwards.
A collection of subsets of a given set which contains the entire set, the empty set, and is closed under arbitrary unions and finite intersections is called a topology for the given set. The sets in this collection are typically referred to as open sets. A set together with a topology is referred to as a topological space.

6.1. If $S$ is a subset of the set of points of a topological space, the collection of subsets of the form $S\cap O$ where $O$ is an open set in the original space becomes a topology for the subset, referred to as the relative topology.

6.2. Note that, if a homeomorphism is not a map of its domain onto its range, then 5.1 is interpreted to mean that the homeomorphism takes open sets in its domain to subsets of the range which are open in the relative topology of the image of the domain.
A topological space is disconnected if it can be partitioned into two non-empty proper subsets, both of which are open. Such a partition is called a disconnection of the space.

7.1. Suppose a disconnected space $S$ is partitioned into two subsets, $A$ and $B$ which are both open. Then $B = Complement(A)$ is closed, and $A = Complement(B)$ is closed, so $S$ is likewise partitioned into two closed sets.
A topological space is connected if it is not disconnected. Equivalently, a space is connected if its only subsets which are both open and closed are the entire space and the empty set.
A subset, $A,$ of topological space $S,$ is connected if it is connected as a topological space with the relative topology inherited from $S.$
A Jordan arc is a homeomorphic image of a closed, bounded interval. A Jordan curve is a homeomorphic image of a circle. A Jordan polygonal curve, or Jordan polygon, is a Jordan curve composed of a finite collection of line segments, which intersect only in their endpoints. A Jordan polygonal arc is similarly a Jordan arc composed of a finite collection of line segments, again intersecting only in their endpoints.
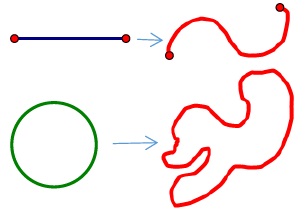
A set is path-connected if, for any two points in the set, there is a Jordan arc in the set whose endpoints are the two given points.

11.1. A closed interval in $\mathbb{R}$ is connected – if not, consider the subset in the disconnection containing the left-hand endpoint. Since this subset is open, it cannot contain its least upper bound; but if the least upper bound of this subset lies in the other subset of the disconnection, which is also open, it lies within an interval of points of the other subset, and hence cannot be the least upper bound of the first subset.

11.2. The continuous image of a connected set is connected – if not, the inverse images of a disconnection would disconnect the domain of the function.

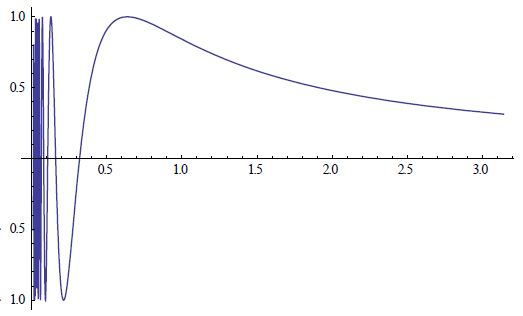
11.3. The classic example of a set which is connected but not path-connected is the "topologist’s sine curve", $y = sin (1/x),$ for $0 \lt x \lt\pi,$ together with the vertical segment from $(0,-1)$ to $(0,1).$

11.4. However, a set which is path-connected is always connected: if not, pick points $x$ and $y$ in distinct subsets $A$ and $B$ which disconnect the set $S.$ Then there is a path from $x$ to $y$ in $S.$ But the intersections of this path with $A$ and $B$ would form a disconnection of the path, which must be connected, as it is the continuous image of a closed interval.

11.5. But an open, connected set in the plane is always path-connected: Let $Q$ be such a set, and pick a point $x$ of the set and consider the subset $S$ which is path-connected to $x.$ Then any other point, say $y,$ in $S$ can be enclosed in an open disc within $Q,$ and any point in such a disc can be connected to $x$ by extending the path from $x$ to $y$ with a segment within the disc. Thus $S$ is open. Similarly, any disc in $Q$ surrounding a limit point in $S$ must intersect $S,$ and, as above, the limit point can be connected to $x$ by extending a path in $S$ with a segment in the disc, so $S$ must be closed. But the only non-empty subset of $Q$ which is both open and closed is $Q$ itself, so $S$ must coincide with $Q:$

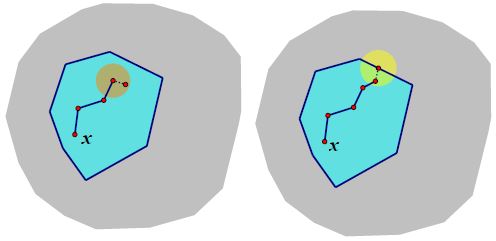
Indeed, any two points of an open, connected subset of the plane can be connected by a Jordan polygonal arc which lies entirely within the set.

11.6. We begin by recalling the basic facts about compact sets in the plane:

11.7. A set is compact if every collection of open sets, whose union contains the set, in fact contains a finite subcollection of open sets whose union also contains the original set. ("Every open cover admits a finite sub-cover.")

11.8. The Heine-Borel Theorem states that any closed, bounded subset of the plane is compact. A proof can be had by the method of successive bisections: Fix an open cover of the set; enclose the set in a rectangle, and subdivide the rectangle into congruent rectangles, each with sides half as long as those of the original rectangle. If each sub-rectangle admits a finite sub-cover, we are done; if not, select one subrectangle which does not. Subdivide that rectangle again, and continue the process to obtain a nested sequence of rectangles, each of which can be covered only by an infinite sub-collection of the original cover. Because the set is closed, this sequence must converge to a single limit point, say, $x.$ But $x$ can be covered by a single open set from the open cover, which will cover the entirety of some small rectangle in the nested sequence. This contradicts the construction of the nested sequence.

11.9. Compactness is a very powerful notion, which is repeatedly invoked in proving Jordan Curve Theorem.

11.9.1. The continuous image of a compact set is compact – for any open cover of the image, consider the collection of the inverse-images of the open sets. These form an open cover of the original compact set in the domain, which by hypothesis admits a finite sub-cover. The open sets in the image which correspond to those in the finite sub-cover will cover the entire image set, confirming that the image, too, is compact.

11.9.2. In particular, a closed interval and a circle are compact sets, thus so, too, are a Jordan curve and a Jordan arc.

11.10. Consider now an open, connected set in the plane. As such a set is path-connected, there is a Jordan arc within the set which connects any two points in the set, say, $x$ and $y.$ Cover this arc with open discs which lie within the open, connected set, with centers on the arc. Since the Jordan arc is compact, a finite subset of this collection of open discs covers the arc (if not already present, add discs centered on each of $x,$ $y).$ Then we can draw a polygonal Jordan arc from $x$ to $y$ in the open, connected set, by connecting the centers of successive discs. [It is possible that this polygonal curve may self-intersect, but in this case, it is easy to excise any of the loops which thus arise to obtain a legitimate polygonal Jordan arc.]

11.11. We will also use the "Extreme Value Theorem" for compact sets: a continuous function $f$ from a compact set $S$ to $\mathbb{R}$ attains maximum and minimum values on $S.$

Cover $\mathbb{R}$ with a sequence of increasing bounded open intervals $\{(-n, n)\}.$ Then the inverse images of these intervals form an open cover of $S.$ Since $S$ is compact, a finite subset of these inverse images suffices to cover $S.$ Then the largest of the intervals $(-n, n)$ whose inverse image is used in the finite sub-cover contains the entire range of the function – that is, the range of the function $f$ must be a bounded set. Let $b$ be the least upper bound of the range. If no point of $S$ is mapped to $b,$ then the function $g(x) = 1/(f(x) – b)$ is continuous on $S$ and must likewise be bounded. But $f$ must take values arbitrarily close to $b,$ as $b$ is the least upper bound of $f(S),$ contradicting the boundedness of $g.$ Thus some point of $S$ must map to $b$ as claimed; the proof for the greatest lower bound is similar.

11.11.1. In particular, the distance between two disjoint compact sets must take on a minimum value; a curve which remains within this distance of one of the sets cannot intersect the other.

11.12. We have shown that a closed, bounded set is compact. Evidently, a compact set is bounded, by the nested interval argument in 11.11. (For a compact subset of $\mathbb{E},$ use nested open discs of radius $n.)$ In fact, a compact set is also necessarily closed: consider a point $x$ in the complement of a compact set $C.$ For each point $y$ in $C,$ one can draw disjoint open discs about $x$ and $y,$ each with radius less than half the distance between them. Then the union of the discs about the points in $C$ form an open cover of $C,$ and the intersection of the discs about $x$ contains $x,$ and is disjoint from $C.$ But since $C$ is compact, only a finite subset of the open cover is needed to cover $C;$ the intersection of the finite collection of discs about $x$ corresponding to the discs in the finite subcover is then an open set containing $x,$ disjoint from $C.$ Thus the complement of $C$ is open, and $C$ must be closed.

11.13. A closed subset of a compact set is compact: If $C$ is compact, and $K$ a closed subset of $C,$ add the complement of $K$ to any open cover of $K$ to obtain an open cover of $C.$ This admits a finite subcover of $C,$ which of course also covers $K.$ Removing the complement of $K$ from this subcover (if necessary), one obtains a finite subcover of $K$ which is a subset of the original open cover of $K.$

11.14 A continuous 1-1 function whose range is a subset of $\mathbb{R}$ or $\mathbb{E}$ need not in general have a continuous inverse. However, if the domain is compact the inverse function is necessarily continuous, and the function must be a homeomorphism. It suffices to show that the function carries closed sets forward: consider a closed subset of the domain. By 11.13, such a set is necessarily compact; by 11.9.1 its image is compact, and therefore, by 11.12, it is closed.

[Thus it is unnecessary to separately assume that the mapping from an interval or circle to a Jordan arc or Jordan curve has a continuous inverse – this follows from the assumptions that the mappings are continuous and 1-1.]
The interior of a set is the union of all its open subsets; equivalently it is its maximal open subset.
The closure of a set is the intersection of all the closed sets which contain it as a subset; it is the smallest closed set which contains it.
The boundary of a set is its closure minus its interior, or, equivalently the intersection of its closure with the closure of its complement:
14.1 Since the open sets in the interior of a set $A$ are the complements of the closed sets which contain the complement of $A,$ it follows that the interior of $A$ equals the complement of the closure of the complement of $A,$ or

$int(A) = compl(closure(compl(A))).$

Thus

$\begin{align} boundary(A) &= closure(A) \setminus int(A)\\ &= closure(A) \setminus compl(closure(compl(A))) \\ &=closure(A) \cap closure(compl(A)). \end{align}$

Thus the boundary of a set and the boundary of its complement coincide.
A component of a set is a maximal connected subset.

15.1 The components of any set are always closed: If a set is connected, its closure is also connected, as every disc surrounding a point of the boundary intersects the set. Thus the closure of a component is a closed connected set containing the component; since the component is a maximal connected set, it must coincide with its closure, and thus be itself a closed set.

15.2 Moreover, in the plane, every component of an open set is open – if $x$ is a point in a component of an open set, it can be surrounded by a disc in the open set, and the union of this disc with the component is connected, and thus the disc must lie in the component, as it is a maximal connected set. Thus the component is itself open.

15.3 A subset separates a superset if the complement of the subset in the superset is disconnected. If $x$ and $y$ are points in the complement of a subset, then the subset separates the points $x$ and $y$ if they are elements of different components of the complement.

15.3.1 If a set separates $x$ and $y,$ then any superset which omits $x$ and $y$ also separates $x$ and $y,$ as the components containing $x$ and $y$ must remain disjoint.

15.3.2 If a set omits $x$ and $y,$ and does not separate $x$ and $y,$ then no subset separates $x$ and $y,$ as enlarging the complementary component containing $x$ and $y$ cannot separate them.

Jordan Curve Theorem, Proof

71535583