Jordan Curve Theorem, Proof
- JCT - Topology Toolbox
- JCT - Prologue
- JCT - Simple Cases
- JCT - Abstract Graphs and Euler’s Formula
- JCT - K3,3 and the Crossed Arcs Lemma
- JCT - Jordan Separation - the general case
- JCT - Boundaries of the components of the complement of a Jordan curve - I
- JCT - The Jordan Arc theorem
- JCT - Boundaries of the components of the complement of a Jordan curve II
- JCT - Uniqueness of the bounded component of the complement
- JCT - K3,3 on a Torus or Moebius Strip
- JCT - Sources
JCT - The Jordan Arc theorem
Scott E. Brodie, MD, PhD
Icahn School of Medicine at Mount Sinai
New York
Lemma
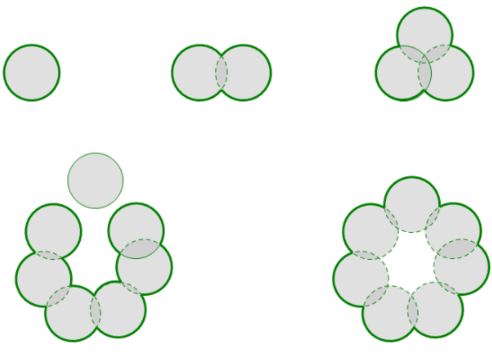
For a connected, finite union of open discs, no two of which are mutually tangent , the outer boundary (which separates the union from the unbounded component of the complement of its closure) is a Jordan curve.
Consider such a connected finite union of open discs. The boundary of the collection includes the boundary of the unbounded component of the complement of the union. This "outer boundary" is composed of subarcs of the collection of circles which bound the discs contained in the finite union. The union of these subarcs is a Jordan curve. This is readily seen by induction on the number of discs, upon the observation that each the boundary circle of each additional disc must intersect the assembly of boundary circles in an even number of points, regardless of whether the disk intersects only contiguous discs, or not, so that it is impossible to have a "free end" of a boundary circle at any point in the induction.
Another Lemma: Two Jordan arcs in a rectangle:
Suppose two disjoint Jordan arcs lie within a rectangle such that one arc intersects the boundary of the rectangle only at one point on the left hand side of the rectangle, and the other intersects the boundary of the rectangle only at one point of the right hand side of the rectangle. Then one can draw an arc from the top of the rectangle to the bottom which does not intersect either arc.
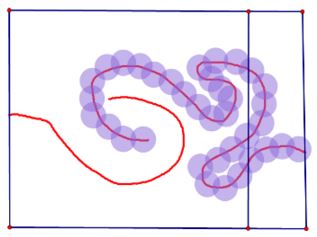
Draw a vertical line from the top to the bottom of the rectangle closer to the right-hand side than any point of the arc which intersects the left-hand side. If vertical line omits the arc which intersects the right-hand side, we are done; If not, cover the right-side arc with a finite, connected, collection of open discs, none mutually tangent, which do not intersect the left-side arc.
The outer boundary of this collection is a Jordan curve. Now construct a compound arc beginning with the vertical segment until it meets the outer boundary of the collection of discs; then continue along the outer boundary (in the direction which does not intersect the rectangle) until the last intersection of the vertical line with the outer boundary; then continue along the vertical line until the bottom of the rectangle is reached. The compound arc satisfies the requirements of the Lemma.
Proof of the Jordan Arc Theorem
A Jordan arc does not separate the plane.
Suppose otherwise. Then the complement of the arc must include at least one bounded component.
The boundary of this component must be a closed subset of the arc. If it is not the entire arc, it must be contained within a subset of the arc, and via the ordering inherited from the underlying closed interval, we can dentify the greatest lower bound and least upper bound for the boundary, which, as a closed set, must include its endpoints.
Directing attention to this minimal arc containing the boundary, identify the points of maximal separation $(A, B),$ and place them on a horizontal line; Surround the curve with a rectangle, with $A,$ $B$ falling on the left and right sides of the rectangle, respectively. Let $C,$ $D\;$ be the endpoints of the arc. By the Lemma above, if $C, D$ are not coincident with $A, B,$ we can draw an arc from the upper side of the rectangle to the lower side, say $EF,$ which does not intersect subarcs $AC$ and $BD.$ (If $C$ or $D$ coincides with $A$ or $B,$ $EF$ should omit $A$ and/or $B.)$
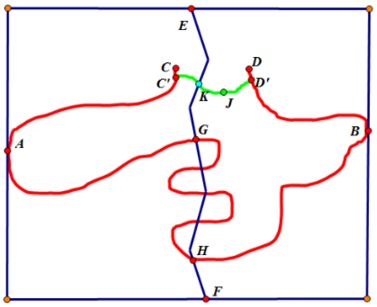
By the Crossed Arcs Lemma, $EF$ intersects $AB,$ say, for the first time at $G$ and the last time at $H.$ Splicing together the subarc $GH$ of $AB$ with the initial and final portions of $EF,$ we obtain a compound arc $EGHF;$ this arc cannot meet the bounded component of the complement of $CD$ – as this would constitute a path connecting the bounded component to the unbounded component, which would then have to coincide; the middle portion $GH,$ as a subarc of $AB,$ is complementary to the bounded component.
Now pick a point, $J,$ in the bounded component; connect it with arcs within the bounded component to accessible points $C'$ and $D'$ of the boundary, near $C$ and $D.$ Then by the Crossed Arcs Lemma, the compound arc $AC'D'B$ must intersect $EGFH$ in a point, $K,$ in the bounded component (as $EF$ is by construction disjoint from arcs $AC$ and $BD;$ and the interior of arc $C'D'$ lies by construction in the bounded component.) But the compound arc $EGHF$ is disjoint from the bounded component – the contradiction confirms that $CD,$ and thus the original Jordan arc, does not separate the plane.
Jordan Curve Theorem, Proof
- JCT - Topology Toolbox
- JCT - Prologue
- JCT - Simple Cases
- JCT - Abstract Graphs and Euler’s Formula
- JCT - K3,3 and the Crossed Arcs Lemma
- JCT - Jordan Separation - the general case
- JCT - Boundaries of the components of the complement of a Jordan curve - I
- JCT - The Jordan Arc theorem
- JCT - Boundaries of the components of the complement of a Jordan curve II
- JCT - Uniqueness of the bounded component of the complement
- JCT - K3,3 on a Torus or Moebius Strip
- JCT - Sources
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73549314
