A Note on Cavalieri's Indivisibles
The great mathematicians of the sixteenth and seventeenth centuries are often seen [Alexander, 7-18] as voyagers who imbibed the atmosphere of the exploration and discovery that prevailed in the natural sciences of that period:
Mathematics, for them, is a science of discovery: it is about the uncovering of secret and hidden gems of knowledge. Its goals have little in common with traditional Euclidean geometry and much in common with the aims and purposes of the newly emerging experimental sciences.
In this spirit Bonaventura Cavalieri (1598-1647) gave a proof of a simple statement of congruence of the two triangles cut off a rectangle by one of the diagonals:
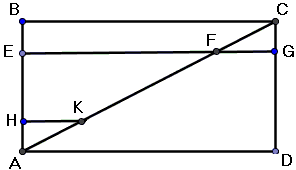
The two triangles - ABC and CDA - are seen is consisting of parallel lines, HK one and FG the other. And, since the lines are pairwise equal, so are the triangles.
To Kepler, Galileo, Cavalieri, Roberval, Herriot, Torricelli a line consisted of indivisble points, a plane of indivisble lines. There was no strict definition of "indivisible" but that did not stop the mathematicians from applying loosely understood notions for establishing some properties - volumes, areas, centers of gravity - of geometric shapes. Cavalieri formulated (1635) two statements that became known as Cavalieri's principles [Eves, 207-208]:
If two planar pieces are included between a pair of parallel lines, and if the lengths of the two segments cut by them on any line parallel to the including lines are always in a given ratio, then the areas of the two planar pieces are also in this ratio.
If two solids are included between a pair of parallel planes, and of the areas of the two sections cut by them on any plane parallel to the including planes are always in a given ratio, then the volumes of the two solids are also in this ratio.
Not surprisingly Cavalieri's seminal work was titled Geometria indivisibilibus. There is a plain demonstration of Cavalieri's 3D principle A diagram (courtesy of wikipedia commons) illustrates an application of Cavalieri's principle to calculations of the volume of a sphere.
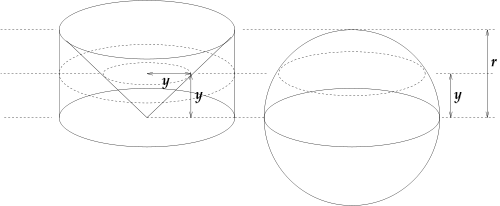
Consider a right cylinder of the radius and height equal to the radius R of the sphere. A right cone inscribed into the cylinder has the remarkable property of complementing the volume of the hemisphere to that of the cylinder. To see that, compare the areas of a circular region and that of the annulus drawn at the same height. They are equal. Therefore, according to Cavalieri's principle the volumes of the two figures are also equal. Since the volume of the cylinder equals πR³ and the volume of the cone is πR³/3, the volume of the hemisphere is 2πR³/3 and the volume of the sphere 4πR³/3.
For the mathematicians who employed the method of indivisibles, the mere fact that it produced correct results was a sufficient guarantee of its validity. Not that they were not aware of possible pitfalls. I believe it was Galileo who observed that two segments of different lengths could be brought into a point-to-point correspondence.
He, like Torricelli after him, believed that indivisibles might come in different sizes. Torricelli came up with a paradox based on a modified Cavalieri's diagram.
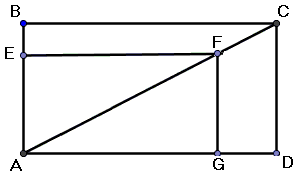
Assume in 2×1 rectangle ABCD point P is chosen on the diagonal AC. For the perpendiculars FE and FG to the sides AB and AD, respectively,
The lack of rigorous foundations did not deter mathematicians from using the indivisibles. Even Newton and Leibniz - the creators of Calculus - had no formal justification for their methods. This was established by Cauchy, Weierstrass, Dedekind and other mathematicians of the nineteenth century.
References
- A. Alexander, From Voyagers to Martyrs: Toward a Storied History of Mathematics, in Circles Disturbed, A. Doxiadis, B. Mazur (eds), Princeton University Press, 2012
- H. Eves, Great Moments in Mathematics Before 1650, MAA, 1983
- M. Kline, Mathematical Thought: From Ancient to Modern Times, v. 1, Oxford University Press, 1972
- What Is Infinity?
- What Is Finite?
- Infinity As a Limit
- Cardinal Numbers
- Ordinal Numbers
- Surreal Numbers
- Infinitesimals. Non-standard Analysis
- Various Geometric Infinities
- Paradoxes of Infinity
- Achilles and the Tortoise
- Tristram Shandy's Paradox
- Infinity and Probability
- Infinite Border, Finite Area
- Rectilinear Paradox
- Infinite Rod
- A Note on Cavalieri's Indivisibles
- Is a Point a Part of a Line?
|Contact| |Front page| |Contents| |Up| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73574026
