What Is Indirect Proof?
One of the methods of proof, is "reductio ad absurdum" - assuming what is to be proved false and getting a contradiction as a result.
As a first (very simple) example, consider proving that, for positive integers $a$ and $b,$ $a^{2}-4b^{2}\ne 1.$
Indirect proof: Assume - on the contrary - that for some positive integers $a$ and $b$, $a^{2}-4b^{2}=1.$ We would have then $(a-2b)(a+2b)=1,$ which splits into two cases: either $a-2b=a+2b=1$ or $a-2b=a+2b=-1.$
In the first case, adding up the two equations gives $2a=2,$ or $a=1$ which leads to $b=0,$ the solution that has been already rejected.
In the second case, adding the two equations gives $2a=-2,$ or $a=-1,$ with negative $a.$
Thus the assumptions proves to be false, implying that its negation - the original claim - is true.
In elementary mathematics, "reductio ad absurdum" is often the simplest way to establish that one condition is necessary and sufficient for another condition to hold. For example, in a right triangle we have the Pythagorean theorem: $a^{2}+b^{2}=c^{2},$ where $a,b$ are the legs, $c$ the hypotenuse of the triangle. I wish to prove the converse: if in a triangle with sides $a,b,c$ $a^{2}+b^{2}=c^{2}$ then the angle opposite $c$ is right. Assume this is false, i.e., that the angle opposite $c$ is not right. We then can erect a perpendicular to, say, $b$ and place $a$ on that perpendicular:
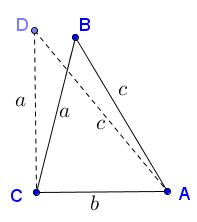
By the Pythagorean theorem, the third side of the just constructed right triangle equals $c$ which means that there are now two distinct triangles with the same three sides, in contradiction to the SSS criterion.
As another example, we know that two angles inscribed in the same circle and subtended by the same arc are equal. To prove the converse, assume there are two equal angles $ABC$ and $AB'C,$ with not concyclic $A,B,B',C.$ This means that $B'$ does not lie on the circle $(ABC)$ passing through $A,B,C.$ Consider just one case where $B'$ lies outside the circle so that $CB$ crosses the circle at $D$ as shown (there are certainly other possibilities to consider):
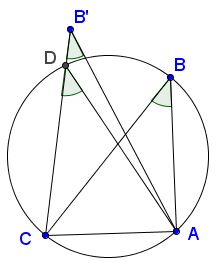
In this configuration, $\angle ADC$ is exterior to $\Delta ADB'$ such that
$\angle ADC=\angle AB'D + \angle B'AD=\angle ABC + \angle B'AD\gt\angle ABC.$
But this contradicts the fact that both $ABC$ and $ADC$ are inscribed into the same circle and ought to be equal by the direct theorem.
Here's a list of additional examples:
- Square root of 2 is irrational
- Infinitude of Primes
- A Property of Cubic Equations
- Pigeonhole Among Friends
- Many Jugs to One I
- Clubs in a Vector Space
- Carpets in Hexagon
- Conic from Parallel Chords
- Existence of the Circumcenter, Indirect Proof
- Sylvester's Problem, Kelly's solution
- Sylvester's Problem, Lang's solution
References
- G. Polya, How to Solve It, Princeton University Press, 1973
- P. Brown, Proof, 2010, www.pbperth.com
Related material
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|Contact| |Front page| |Contents| |Algebra| |Up|
Copyright © 1996-2018 Alexander Bogomolny
73563208
