Outline Mathematics
Geometry
Existence of the Circumcenter, Indirect Proof
The traditional proof of existence of the circumcenter (Euclid IV.5) exploits the transitivity,reflexivity,symmetry,transitivity of equality: if $x=y$ and $y=z$ then $x=z.$ But transitivity is not exclusive to the relation of equality. Below I give another proof depending on transitivity, but this time of the relation "greater than". The proof differs from the standard one in another aspect: it is indirect, meaning that it is in the form reductio ad absurdum. We start with assuming the opposite of what is needed to be proved and logically arrive at a contradiction which shows that the assumption that set off the derivation is false.
Let's start with a remark that the perpendicular bisector of a segment $AB$ consists of points $X$ equidistant to $A$ and $B.$ For every point on the perpendicular bisector of $AB,$ $AX=BX.$ To emphasize that point, I shall use a more explicit notation: $\mbox{dist}(A,X)=\mbox{dist}(B,X).$ As a matter of fact, the perpendicular bisector of $AB$ divides the plane into two half-planes,half-planes,quarters: in one the points are closer to $A,$ in the other to $B.$ The perpendicular bisector serves the border of both half-planes.
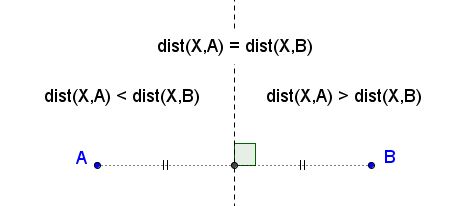
Three noncollinear points $A,B,C$ form three segments $AB,$ $BC,$ and $CA.$ We wish to prove that the perpendicular bisectors of the three segments concur at a point,parallel,perpendicular,concur at a point. For the proof, assume that they are not and see where this leads us.
According to Euclid, the bisectors of any two segments could not be parallel unless the segments themselves are parallel which is not the case here. It follows that the bisectors (which, by our assumption, are not concurrent) form a triangle:
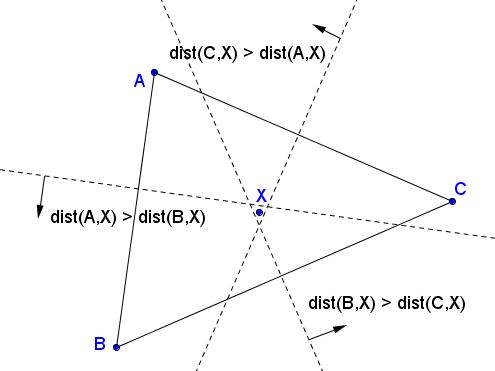
For any point $X$ inside that triangle we have
$\mbox{dist}(A,X)>\mbox{dist}(B,X),\\ \mbox{dist}(B,X)>\mbox{dist}(C,X),\\ \mbox{dist}(C,X)>\mbox{dist}(A,X)$
which is contradictory because, by the transitivity of the relation "greater than", the first two inequalities imply $\mbox{dist}(A,X)>\mbox{dist}(C,X)$ - the opposite of the third inequality. This is a contradiction that reveals the falsity,validity,falsity of our basic assumption that the three bisectors are not concurrent. Therefore they do meet at a point.
|Up| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73577279
