Conic from Parallel Chords

What Might This Be About?

Problem

Two circles intersect at points $A$ and $B.$ Chords $EF$ on one and $GH$ on the other are parallel.

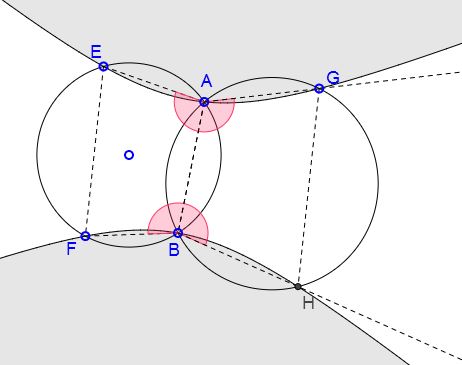
Conic from Parallel Chrods - problem

Prove six points $A,B,E,F,G,H$ lie on a conic.

Solution

The easiest way to prove the statement is to show that it is equivalent to its inverse. This is done in a reasonably standard manner by reductio ad absurdum.

There is a conic through five points, $A,B,E,F,G$ which we assume misses H. Assume that instead the conic crosses the second circle in $A,B,H',G.$ The quadrilateral $ABH'G$ is then cyclic, with six points $A,B,E,F,G,H'$ lying on the same conic. By the converse statement, $GH'\parallel EF.$ Since both $GH$ and $GH'$ happen to be parallel chords in the same circle, we conclude that $H'=H,$ thus arriving at a contradiction with our assumption.

Converse

Given six points on a conic, $A,B,E,F,G,H.$ Such that $ABFE$ and $EBHG$ are cyclic quadrilaterals. Then $EF\parallel GH.$

This has been shown previously.

Acknowledgment

The problem has been posted by Dao Thanh Oai at the CutTheKnotMath facebook page.

72111968