Sylvester's Problem, Lang's Solution
The Sylvester Problem has been posed by James Joseph Sylvester in 1893 in Educational Times:
Let $n$ given points have the property that the line joining any two of them passes through a third point of the set. Must the $n$ points all lie on one line?
The dual of the stated theorem appears easier to prove:
Let $n$ given coplanar lines have the property that through the point of intersection of any two there passes a third. Then $n$ lines are concurrent.
Solution
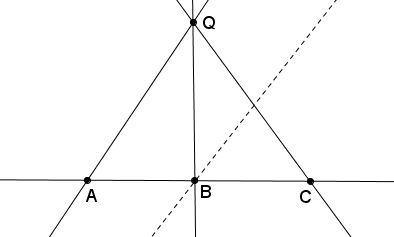
Suppose the theorem false. Parallelism may be removed by projection. Consider one line $p$ of the set. Not all intersections lie on $p.$ There is a nearest intersection $Q$ which is not on $p.$ Through $Q$ there pass at least three lines $a,b,c,$ meeting $p$ in $A,B,C,$ say. Suppose $B$ lies between $A$ and $C.$ There is anther line $d$ passing through $B$ and hence entering the triangle $ACQ.$ Hence $d$ must cut the interval $AQ$ or the interval $CQ,$ contrary to the definition of $Q.$
References
- G. D. W. Lang, The dual of a well-known theorem, Math. Gazette 39 (1955), p. 314.
- J. J. Sylvester, Educational Times, Mathematical Question 11851, vol. 59 (1893), p. 98
|Contact| |Front page| |Contents| |Algebra| |Up|
Copyright © 1996-2018 Alexander Bogomolny
73537921
