Sylvester's Problem, Kelly's Solution
The Sylvester Problem has been posed by James Joseph Sylvester in 1893 in Educational Times:
Let $n$ given points have the property that the line joining any two of them passes through a third point of the set. Must the $n$ points all lie on one line?
L. M. Kelly discovered his proof somewhere between 1944 (when Steinberg's and Gallai's proofs appeared in print) and 1948 (when H. S. M. Coxeter presented it in his article.) I could not find the exact source, or date it exactly.
Solution
Given the set $\Pi$ of noncollinear points, consider the set of lines $\Sigma$ that pass through at least two points of $\Pi.$ Such lines are said to be connecting. Among the connecting lines, those that pass through exactly two points of $\Pi$ are called ordinary.
Any point in $\Pi$ and any connecting line in $\Sigma$ not through the point determine a perpendicular distance from the point to the line. The collection of all these distances is finite, because $\Pi$ and $\Sigma$ are finite, so there is a smallest such distance. Let $p'$ (in $\Pi)$ and $s'$ (in $\Sigma)$ be a nonincident pair which realizes this smallest distance. Then $s'$ is ordinary! For otherwise $s'$ would contain at least three points of $\Pi$ and two of them would have to lie on the same side of $q,$ the foot of the perpendicular from $p'$ to $s',$ as below
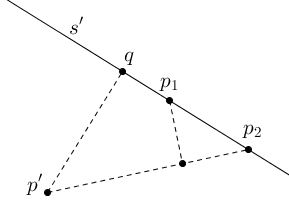
where the two points on the same side of $q$ are $p_1,$ $p_2,$ with $p_1$ between $q$ and $p_2$ $(p_{1} = q$ is a possibility). Now the distance from $p_1$ to the connecting line $p'p_2$ would be smaller than the distance from $p'$ to $s'.$
Note that Kelly's proof serves a characteristic application of the Extremal Principle in problem solving.
References
- M. Aigner, G. Ziegler, Proofs from THE BOOK, Springer, 2000
- C. Alsina, R. B. Nelsen, Charming Proofs, MAA, 2010
- P. Borwein, W. O. J. Moser, A survey of Sylvester's problem and its generalizations, Aequationes Mathematicae 40 (1990) 111 - 135
- H. S. M.Coxeter, A Problem of Collinear Points, The American Mathematical Monthly, Vol. 55, No. 1 (Jan., 1948), pp. 26-28
- P. Erdös, R. Steinberg, Problem 4065 [1943, 65]. Proposed by P. Erdös, Princeton, N. J, Solution by Robert Steinberg, Student, University of Toronto, The American Mathematical Monthly, Vol. 51, No. 3 (Mar., 1944), pp. 169-171
- J. J. Sylvester, Educational Times, Mathematical Question 11851, vol. 59 (1893), p. 98
|Contact| |Front page| |Contents| |Algebra| |Up|
Copyright © 1996-2018 Alexander Bogomolny
73569534
