What Is Counterexample?

Counterexample is an example with a negative connotation. Whereas an example may be used to support or illustrate a claim, a counterexample is used to refute an assertion. How an example is being used often depends on the purpose or the formulation. For example, the word "nth" is an example of an English word without a vowel. It is a counterexample to the claim that every English word contains a vowel.

To prove that $A\subset B$ one has to show that every element $a\in A$ has a characteristic property of elements of $B.$ To show that the inclusion does not hold, one needs to exhibit just one element $a\in A$ that does not belong to $B$ - this element would serve a counterexample to the assertion $A\subset B.$ In the above example,

• $A$ is the set of all English words,

• $B$ is the set of all English words that contain at least one vowel.

To give another example (this one I learned from Patrick Honner), recollect a characterization of parallelogram as a quadrilateral with two pairs of parallel sides. It is a straightforward matter to prove that parallelogram admits two other (and several more) characterizations:

1. Quadrilateral with two pairs of equal opposite angles is a parallelogram.

2. Quadrilateral with two pairs of equal opposite sides is a parallelogram.

By borrowing a half from each and combining, it is natural to inquire whether, and perhaps even conjecture that,

A quadrilateral with a pair of equal opposite sides and a pair of equal opposite angles is a parallelogram.

Patrick's construction serves a counterexample to this conjecture:

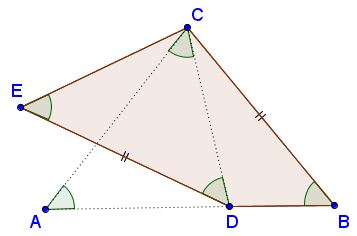
(Start with an isosceles $\Delta ABC;$ make a similar $\Delta ACD;$ reflect the latter in the perpendicular bisector of $CD$ to obtain quadrilateral $BCED,$ with $\angle DBC=\angle CED$ and $BC=DE.$)

As a problem-solving technique, looking for a counterexample often helps crystallize the importance of problem's data, especially when some parts of the data are omitted.

In the opinion of B. R. Gelbaum and J. M. H. Olmsted - the authors of two popular books on counterexamples - much of mathematical development consists in finding (and proving) theorems and counterexamples.

Here's a list of pages at this site where counterexamples popped up, were sought for, and have been found useful.

• A number is written with $81$ ones. Prove it's a multiple of $81$
• Every English word contains at least one vowel
• Ramsey number $R(4,4)$ exceeds $17$
• Characterization of orientable rectangle
• Integers below $126$ but not $127$
• Grünbaum's counterexample to Erdös' conjecture
• Stones in Cups
• Every simple polyhedron admits a triangulation
• Circles separating points
• Monotone increasing function with almost everywhere zero derivative
• Sum of distances from a point to the sides of an $n$-gon independent of the point
• Releasing birds from cages
• Malfatti's circles are optimal
• Covering a chessboard with domino
• Second $4\times 4$ Coloring Problem
• Trisecting an angle
• A Curious Property of Numbers 3 and 5

Reference

1. B. R. Gelbaum and J. M. H. Olmsted, Counterexamples in Analysis, Holden-Day, 1964
2. B. R. Gelbaum and J. M. H. Olmsted, Theorems and Counterexamples in Mathematics, Springer-Verlag

Related material Read more...
	What Is Angle
	What Is Axiom?
	What Is Circle?
	What Is Line?
	What Is Point?
	What Is Theorem?

|Contact| |Front page| |Contents| |Up|

Copyright © 1996-2018 Alexander Bogomolny